Genetische Algorithmen gehören zu der Gruppe der evolutionären Algorithmen und stellen eine Metaheuristik zum Lösen von komplexen Optimierungsproblemen dar. Sie basieren dabei grundlegend auf der iterativen Optimierung über Selektion, Kreuzung und Mutation der stärksten Lösung.[1]
¶ Hintergrund
Der genetische Algorithmus wurde vor allem durch das Buch Adaptation in Natural and Artificial Systems (1975) popularisiert und ist eine Abstraktion der biologischen Evolution auf der Grundlage der natürlichen Selektion.[2] Die Methode basiert somit grundlegend auf genetischen Konzepten. Sie wurde breites auf ein breites Spektrum von Optimierungsproblemen (bspw. Sudoku und Super Mario) angewandt.[3]
¶ Bausteine
¶ Operanden
Die fundamentalen Operanden eines genetischen Algorithmus sind die Population, Chromosome und Gene (siehe Abb. 1). Eine Population besteht aus mehreren Chromosomen. Dabei repräsentiert jedes Chromosom eine Lösung im Suchraum und ist als ein Vektor endlicher Länge von variablen Komponenten (bspw. und ), auch Gene genannt, kodiert.[4]
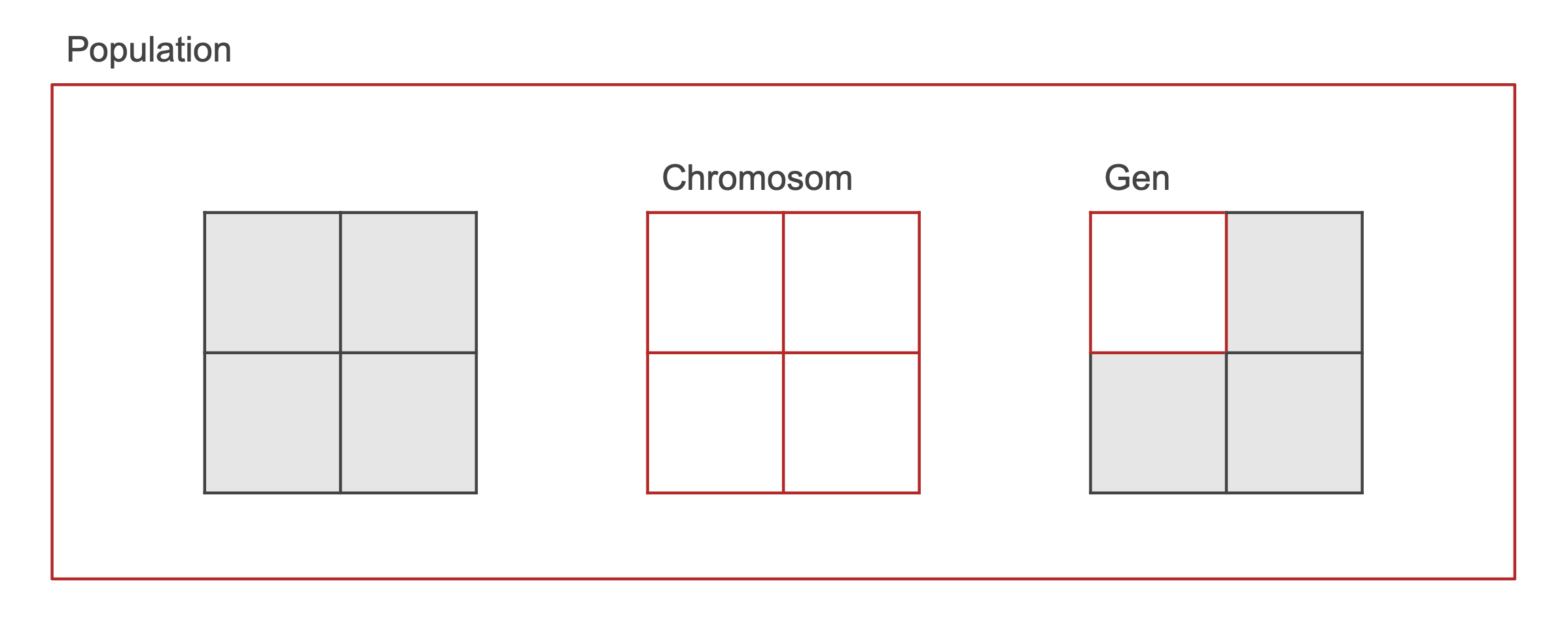
¶ Operatoren
Auf den oben genannten Operanden wird mit den Operatoren Selektion, Kreuzung und Mutation gearbeitet.[4:1]
¶ Selektion
Bei der Selektion wird eine fitnessproportionale Auswahl der Chromosome (genehm einer Fitnessfunktion) getroffen, um gute Gene an nachfolgende Generationen (zukünftige Iterationen des Algorithmus) weiterzugeben.
Ein häufiger Ansatz ist hier die elitäre Auswahl, wobei die Chromosome mit den niedrigsten Fitnessfunktionswerten ausgewählt werden. Die Anzahl ist dabei frei zu wählen. Die Zielfunktion für die Evaluierung der oben genannten Fitness bzw. Fitnessfunktion soll die individuellen Kriterien der Lösung des vorliegenden Optimierungsproblems in mathematischer Form ausdrücken (siehe Sudoku und Super Mario). Die folgende Gleichung nach Bushra Alhijawi und Arafat Awajan definiert die Fitnessfunktion in der einfachsten Form:
es gilt
- als Wert der Zielfunktion des Chromosoms .
- als Durchschnitt der Zielfunktionswerte aller Chromosome in der Population.[1:1]
¶ + Strategie (Anteil von Jan Schäfer)
Die + Evolutionsstrategie, bedient sich beim Elitismus.
- = Größe der Population der Eltern
- = Größe der Gesamten Population
In jeder Generation werden die besten der Population als Elternteil für die nächste Generation festgelegt.
muss ein Vielfaches von sein. So ergibt sich auch aus die Anzahl von Kindern pro Elternteil.[5]
¶ Kreuzung
Bei der Kreuzung werden die Gene mehrerer Chromosomen an bestimmten Kreuzungsstellen ausgetauscht und neue Chromosomen (Nachfolger) entstehen. Für die Auswahl der Kreuzungsstellen selbst gibt es verschiedene Ansätze, darunter vor allem:
- Ein-Punkt-Kreuzung: die Gene werden an einem zufälligen Kreuzungspunkt jeweils ausgetauscht.
- -Punkt-Kreuzung: bei der allgemeinen Form der Ein-Punkt-Kreuzung werden die Gene an zufälligen Kreuzungspunkten ausgetauscht.[1:2]
¶ Mutation
Durch die Mutationen werden zufällige Gene der Nachfolger geändert, um eine Vielfalt in der Population zu erhalten.[4:2] Auch hier gibt es diverse Ansätze der eigentlichen Implementierung. Zwei häufige sind:
- Ein-Punkt-Mutation: ein zufälliges Gen wechselt zu einem zufälligen anderen Wert mit der Mutationswahrscheinlichkeit .
- Bitweise Inversionsmutation: mit der Wahrscheinlichkeit werden alle Gene des Chromosoms invertiert (bspw. zu und zu ).[1:3]
¶ Algorithmus
Bei einem klassischen genetischen Algorithmus muss vorerst eigenständig die Fitnessfunktion definiert werden. Es wird dann mit der (häufig zufallsbasierten) Schaffung einer initialen Population von Chromosomen begonnen.
Für den eigentlichen Evolutionszyklus wird zuerst die Fitness aller Chromosome der aktuellen Population genehm der Fitnessfunktion bewertet. Es erfolgt (bei einer elitären Auswahl) die fitnessproportionale Selektion der fittesten Chromosome mit den niedrigsten Fitnessfunktionswerten. Nun wird eine neue Population über die Kreuzung von ausgewählten Chromosomen und die darauffolgende Mutation geschaffen (siehe Abb. 2). Darauf folgt das Ersetzen der alten Population mit der neuen.
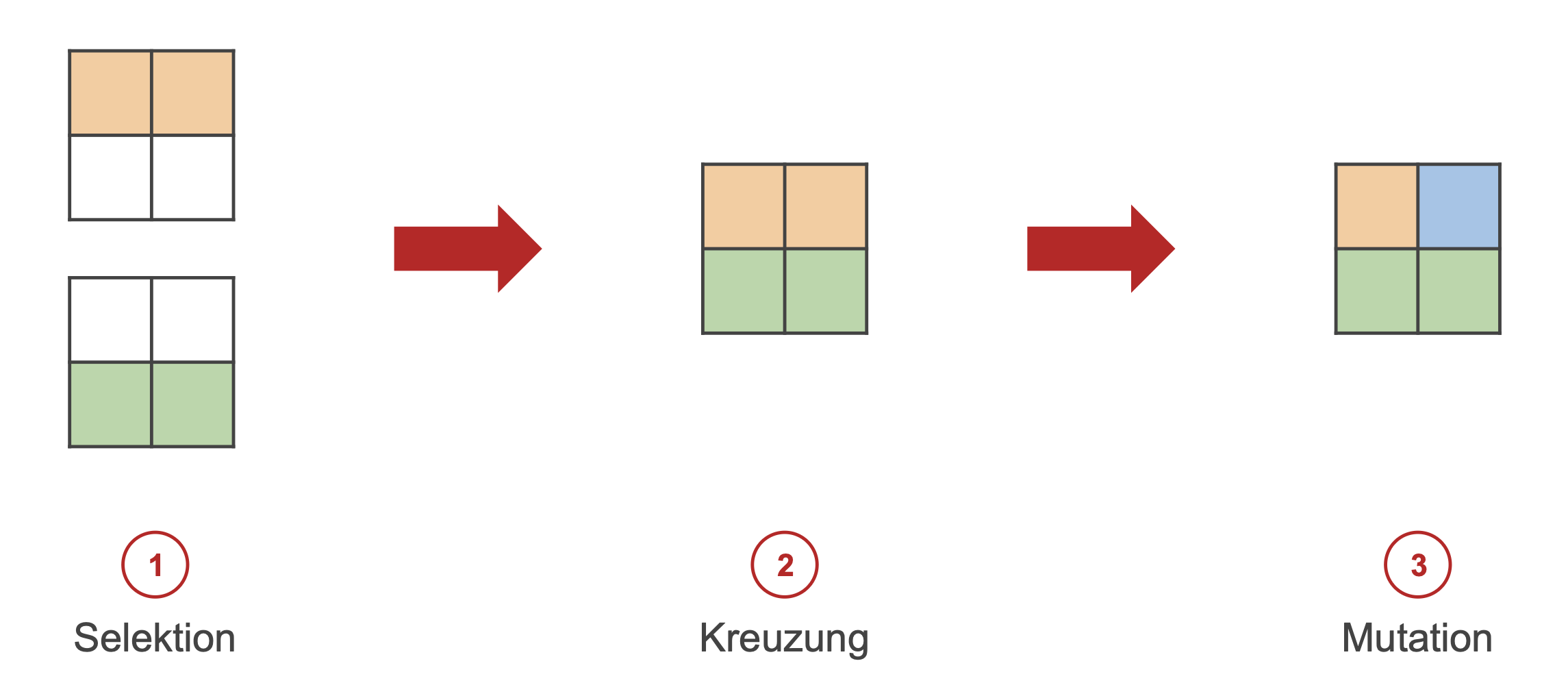
Der Evolutionszyklus wird bis zum Erreichen einer ebenfalls eigenständig definierten Abbruchbedingung (bspw. Anzahl Zyklen) wiederholt. Ist diese Bedingung erreicht, wird das fitteste Chromosom der aktuellen Population zurückgegeben.[4:3][3:1]
¶ Pseudocode
create initial population of chromosomes
while not end condition do
for each chromosome in population
evaluate fitness
select chromosomes with max fitness
perform crossover
perform mutation with propability y
replace old population with new population
select chromosome with max fitness
return chromosome
¶ Bewertung
¶ Herausforderungen
Nachteile sind vor allem die eigenständige Formulierung der Fitnessfunktion, Festlegen der Populationsgröße, sowie die Wahl wichtiger Parameter wie die Mutationswahrscheinlichkeit. Das Festlegen dieser Parameter fällt grundsätzlich unter das Problem der Hyperparameteroptimierung. Dabei ist vor allem die Berechnungszeit und Qualität der Lösung abzuwägen. Im Allgemeinen führen komplexere Strukturen (bspw. eine größere Population) zu einer längeren Berechnungszeit. Diese können zugleich aber auch eine potenziell bessere Lösung hervorbringen, da bei einer größeren Population zum Beispiel auch eine größere Vielfalt innerhalb der Population herrscht und der Suchraum somit breiter erkundet wird.[6]
¶ Möglichkeiten
Ein markanter Vorteil ist die Fähigkeit, mit komplexen Problemen umzugehen. Nach Xin-She Yang basiert dies auf der in hohem Maße anpassbaren Fitnessfunktion, welche das Regelwerk des zugrundeliegenden Optimierungsproblems darstellen soll. Diese kann stationär, nichtstationär, linear, nichtlinear, kontinuierlich oder diskontinuierlich sein.[3:2]
Eine hohe Parallelisierbarkeit ist in vielen Fällen ebenfalls realisierbar. Die verschiedenen Ansätze (bspw. Populationen oder Chromosomen) können sich wie unabhängige Agenten verhalten und den Suchraum der potenziellen Lösungen des jeweiligen Optimierungsproblems in vielen Richtungen gleichzeitig erkunden, so Yang.[3:3]
Möglicherweise stellen evolutionäre Algorithmen im Allgemeinen sogar eine skalierbare Alternative zu Reinforcement Learning dar. Insbesondere sind diese im Vergleich einfacher zu implementieren (u.A. wird keine Backpropagation benötigt), sowie leichter zu skalieren und weisen, aus den oben genannten Gründen, eine höhere Parallelisierbarkeit auf. Dazu gehen evolutionäre Algorithmen besser mit spärlichen Belohnungen (Hinweise auf eine gute Lösung) um.[7]
¶ Referenzen
B. Alhijawi and A. Awajan, “Genetic algorithms: theory, genetic operators, solutions, and applications,” Evolutionary Intelligence, Feb. 2023, doi: https://doi.org/10.1007/s12065-023-00822-6. ↩︎ ↩︎ ↩︎ ↩︎
H. H John, Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence. Ann Arbor: University of Michigan Press, 1975. Accessed: Jan. 31, 2024. [Online]. Available: https://openlibrary.org/books/OL5070129M/Adaptation_in_natural_and_artificial_systems. ↩︎
X.-S. Yang, “Chapter 6 - Genetic Algorithms,” ScienceDirect, Jan. 01, 2021. https://www.sciencedirect.com/science/article/pii/B9780128219867000135. ↩︎ ↩︎ ↩︎ ↩︎
M. Mitchell, “An introduction to genetic algorithms,” Choice Reviews Online, vol. 34, no. 01, pp. 34-035134-0351, Sep. 1996, doi: https://doi.org/10.5860/choice.34-0351. ↩︎ ↩︎ ↩︎ ↩︎
S. Bojarski and C. B. Congdon, “REALM: A rule-based evolutionary computation agent that learns to play Mario | IEEE Conference Publication | IEEE Xplore,” ieeexplore.ieee.org. https://ieeexplore.ieee.org/abstract/document/5593367. ↩︎
S. Katoch, S. S. Chauhan, and V. Kumar, “A review on genetic algorithm: past, present, and future,” Multimedia Tools and Applications, vol. 80, no. 5, Oct. 2020, doi: https://doi.org/10.1007/s11042-020-10139-6. ↩︎
T. Salimans, J. Ho, X. Chen, S. Sidor, and I. Sutskever, “Evolution Strategies as a Scalable Alternative to Reinforcement Learning,” arXiv:1703.03864 [cs, stat], Sep. 2017, Available: https://arxiv.org/abs/1703.03864. ↩︎