¶ Allgemein
Minesweeper ist ein spannendes Einzelspieler-Spiel, bei dem der Spieler durch logisches Denken alle Felder aufdecken muss, ohne eine Mine zu treffen. Das Spiel wurde Anfang der 1990er Jahre von Microsoft entwickelt und erlangte vor allem dadurch Popularität, dass es auf den Windows-Versionen von 3.1 bis Windows 7 vorinstalliert war.[1]
¶ Regeln
¶ Spielprinzip
Es gibt ein n × m großes Spielfeld, das zu Beginn des Spiels komplett verdeckt ist. Unter x dieser verdeckten Felder befindet sich eine Mine. Die Spielfeldgröße und die Anzahl der Minen hängen vom Schwierigkeitsgrad ab. Welche Felder Minen enthalten, ist unbekannt.
Deckt der Spieler ein Feld auf, das keine Mine ist, erscheint auf diesem Feld eine Zahl zwischen 0 und 8 (auch als Label bezeichnet). Diese Zahl gibt an, wie viele der angrenzenden Felder (auch Nachbarn genannt) Minen enthalten. Mit diesem Wissen kann der Spieler im Optimalfall nach und nach das Spielfeld aufdecken. Identifizierte Minen können mit einer Flagge markiert werden. [1:1]
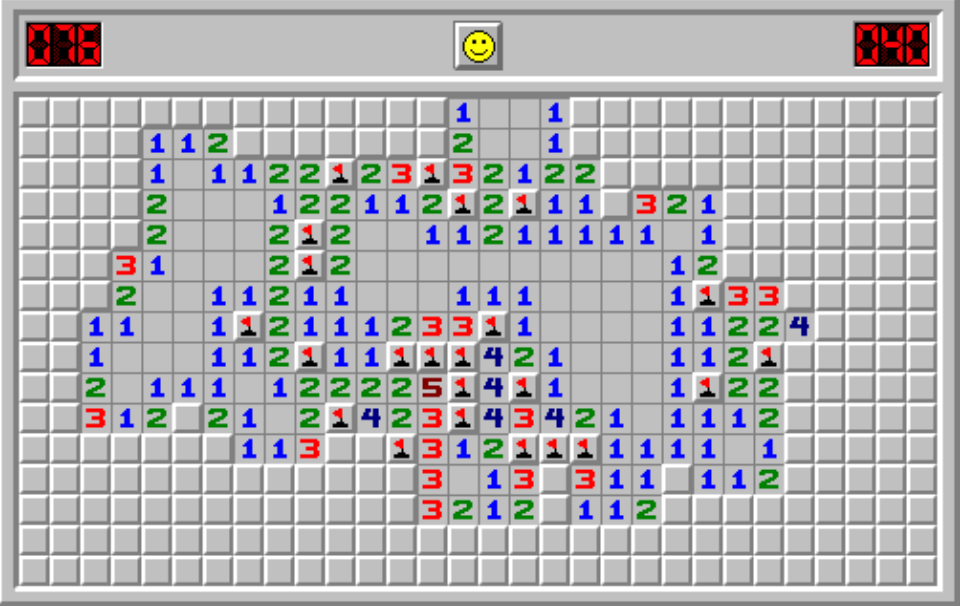
Beispiel Minesweeper-Feld [2]
¶ Ziel des Spiels
Das Ziel des Spiels ist es, alle Felder aufzudecken, die keine Mine enthalten. Wird eine Mine aufgedeckt, verliert der Spieler das Spiel. [1:2]
¶ Schwierigkeitsgrad
Je nach Schwierigkeitsgrad variieren die Größe des Spielfelds und die Anzahl der Minen. Unterschiedliche Implementierungen nutzen verschiedene Stufen, aber für diesen Artikel werden folgende betrachtet:
- Beginner: 9x9 mit 10 Minen
- Intermediate: 15x13 mit 40 Minen
- Expert: 16x30 mit 99 Minen
¶ Unlösbare Stellungen
Trotz der relativ simplen Regeln ist Minesweeper ein sehr schwer zu lösendes Problem und es ist sogar unmöglich immer sicher eine Lösung zu finden. Dies liegt einerseits an den wenigen vorhandenen Informationen zu Beginn des Spiels, aber selbst mit vielen Informationen gibt es Konfigurationen bei Minesweeper, welche nur durch raten gelöst werden können, welche einen oft in 50/50-Entscheidungen zwingen.

Unlösbare Situation [2:1]
Im gezeigten Beispiel konnte bereits eine Mine markiert werden und es ist klar, dass genau ein Feld von A oder B und eines von C oder D eine Mine ist. Doch welches der beiden Felder die Mine enthält kann nicht herausgefunden werden, da keine weiteren Informationen vorliegen. Der Spieler muss raten oder blind ein neues Feld aufdecken.[2:2]
¶ Erster Zug
Der erste Zug bei Minesweeper verdient besondere Beachtung, da das gesamte Spielfeld noch bedeckt ist und der Spieler keinerlei Informationen über die Position der Minen hat. Um diesen zufälligen Zug zu vermeiden, gibt es Implementierungen, bei denen das Spielfeld erst nach dem ersten Zug generiert wird, sodass keine Mine getroffen werden kann.
Unabhängig von der Variante sollte der Spieler nach dem ersten Zug versuchen, möglichst viele Informationen zu erhalten, um nicht erneut einen unsicheren Zug machen zu müssen. Die Implementierung, wobei der erste Zug sicher ist, ist die verbreitetere, deshalb wird diese folgend betrachtet.
Um den besten ersten Zug zu finden, müssen 3 Kategorien an Feldern beachtet werden:
- Felder im Zentrum mit 8 angrenzenden Feldern
- Felder am Rand mit 5 Nachbarn
- Felder in der Ecke mit 3 Nachbarn

Anzahl der Nachbarn, je nach Position [2:3]
Wird ein Feld aufgedeckt, das keine Mine ist, so wird die Anzahl der Minen in der direkten Nachbarschaft angezeigt. Ohne Risiko können neue Felder nur dann aufgedeckt werden, wenn sich 0 Minen in der Nachbarschaft befinden und folgich eine "0" aufgedeckt wird, da in diesem Fall alle angrenzenden Felder sicher sind.
Vor dem ersten Zug sind keine Informationen über die Position der Minen bekannt, weshalb jedes Feld für den Spieler die gleiche Wahrscheinlichkeit hat, eine Mine zu enthalten. Um die Chance zu maximieren, ein Feld ohne Minen in der Nachbarschaft zu finden, sollte ein Feld mit möglichst wenigen Nachbarn gewählt werden. Daher hat der Spieler die größte Wahrscheinlichkeit, eine "0" zu finden, wenn er eine der Ecken zuerst aufdeckt, da diese nur drei Nachbarn haben.
Trotzdem ist es nicht zwingend ein Fehler, zentral oder am Rand zu beginnen. Wird an solchen Stellen eine "0" entdeckt, können mehr Nachbarfelder aufgedeckt werden, was zusätzliche Informationen liefert. Es bleibt somit eine Abwägung zwischen dem Risiko, keine "0" zu finden, und der geringeren Menge an Informationen, die verfügbar wäre, selbst wenn eine "0" aufgedeckt wird.
¶ Andere Lösungsansätze
¶ Single Point Strategie
Single-Point-Solver (SP) gehören zur einfachsten Kategorie von Minesweeper-Solvern, da sie jeweils nur ein einzelnes Feld und dessen unmittelbare Nachbarschaft betrachten. Beim Single-Point-Ansatz gibt es zwei Möglichkeiten, sichere Züge zu identifizieren:
- Fall: Alle Minen in der Nachbarschaft eines Feldes wurden bereits markiert. Daher können alle übrigen Nachbarn als sichere Felder angesehen und aufgedeckt werden.
- Fall: Die Anzahl der noch nicht markierten Minen in der Nachbarschaft entspricht exakt der Anzahl der noch verdeckten Felder, wie durch die Zahl auf dem Feld angegeben. In diesem Fall können alle verbleibenden Nachbarn als Minen markiert werden.
Kann einer der beiden Fälle für ein Feld festgestellt werden, können alle noch bedeckten Nachbarfelder entsprechend markiert oder aufgedeckt werden. Wird jedoch kein solches Feld gefunden, stößt der SP-Ansatz an seine Grenzen, da er keine übergreifenden Zusammenhänge zwischen Feldern erkennen kann. In diesem Fall bleibt als einzige Option, zu raten, um neue Informationen zu gewinnen, und anschließend alle Felder erneut auf die beiden beschriebenen Fälle zu prüfen. [3]
David Baccera hat in seiner Arbeit "Algorithmic Approaches to Playing
Minesweeper" ebenfalls die Single Point Strategie untersucht und hat dabei die folgenden Gewinnraten ermittelt:
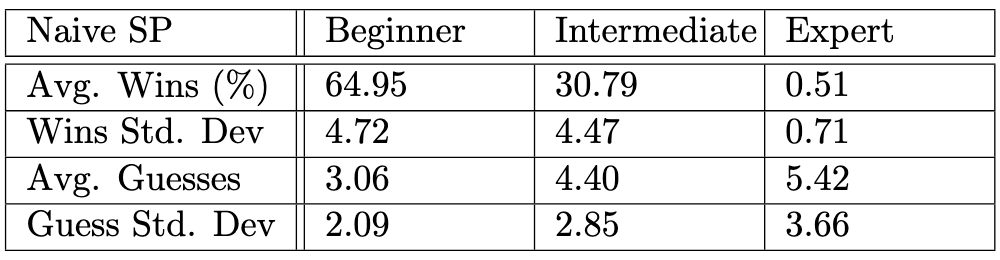
Ergebnisse für SP auf Beginner, Intermediate und Expert [3:1]
¶ Equation Strategie
Die Equation Strategie, welche später als Vergleichsalgorithmus verwendet wird, basiert auf der Implementierung von John D. Ramsdell in seinem Projekt "Programmer´s Minesweeper". Entwicklern, die ihre eigene Strategie entwickeln möchten, wird in diesem Projekt ausdrücklich empfohlen, den Quellcode des Algorithmus nicht zu analysieren. Daher ist nicht bekannt, wie die Equation-Strategie im Detail funktioniert.[4]
¶ Constraint Satisfaction Problem
¶ Allgemein
Ein Constraint Satisfaction Problem oder auch CSP, ist eine mathematische Darstellung eines Problems, welcher aus einer endlichen Menge an Bedingungen (Constraints) besteht, die erfüllt werden müssen um dieses Problem zu lösen.
CSPs können für ein weites Feld an Problemen eingesetzt werden und sind vor allem im Bereich der künstlichen Intelligenz weit verbreitet. [3:2]
Ein CSP wird als Triple dargestellt , wobei:
- ein endliches Set an Varibalen enthält:
X = \
- eine Funktion ist, welche jeder Variable einen Wert zuteilt:
D: X ↦ \{D_1, D_2, ..., D_n\}; xi ↦ D1 \text{ für alle } i \in \
- ist ein endliches Set mit t Bedingungen:
X: C ↦ \{c_1, c_2, ..., c_t\}, Var(c_j) \in X \text{ für alle } j \subseteq \
Ein Constraint besteht aus einer Menge an Variablen, welche mit einem Wert aus dem Wertebereicht belegt werden müssen, um dann über die entsprechende Relation die Bedingung zu erfüllen.
Als Lösung für ein Constraint Satisfaction Problem wird jede zulässige Belegung aller Variablen angesehen, bei welcher alle Constraints erfüllt sind. [2:4]
¶ Angewendet auf Minesweeper
¶ Minesweeper als CSP definineren
Minesweeper wird als CSP wie folgt definiert:
- jedes noch unaufgedeckte Feld ist eine Variable
- der Wertebereich ist , wobei 0 für ein sicheres Feld und 1 für eine Mine steht
- für jedes aufgedeckte Feld wird ein Constraint erstellt, wobei gelten muss:
wobei alle noch unaufgedeckten Nachbarn und die Anzahl der markierten Minen in der Nachbarschaft ist.
¶ Beispiel für Mineseeeper als CSP

Beispiel Situation, um die Darstellung von Minesweeper als CSP zu veranschaulichen[2:5]
Für die oben zu sehende Situation ergibt sich dann folgendes CSP:
X = \
D: X ↦ \
(zur Übersichlichkeit als Tabelle dargestellt und gekürzt)
| Ausgangspunkt | Constraint |
|---|---|
| P | |
| Q | |
| R | |
| S | |
| T | |
| ... | ... |
| Y | |
| Z |
¶ Tiefensuche mit Backtracking zur Lösungssuche
Um aus dem erstellten CSP (Constraint-Satisfaction-Problem) die nächsten Züge zu generieren, wird das CSP einem Solver übergeben. Dieser Solver verwendet eine Tiefensuche mit Backtracking, um alle möglichen Belegungen der Variablen zu finden, die keine Constraints verletzen und somit gültige Lösungen darstellen.
Zu Beginn werden – ähnlich wie beim SP-Algorithmus – alle Variablen belegt, die sicher bestimmt werden können. Das ist der Fall, wenn alle verbleibenden Nachbarn Minen sind oder alle Minen in der Nachbarschaft bereits markiert wurden.
Anschließend werden zuerst die Variablen belegt, die in den meisten Constraints vorkommen. Dadurch können aussichtslose Pfade möglichst früh abgeschnitten werden. Nach der Belegung einer Variable werden alle Constraints, in denen diese Variable vorkommt, überprüft. Wird dabei eine Verletzung festgestellt, wird der alternative Wert der Variable geprüft. Führt auch dieser zu einer Verletzung, wird Backtracking ausgelöst. Die Tiefensuche durchläuft so den gesamten Suchbaum. Sobald eine Lösung gefunden wird, bei der alle Variablen belegt sind und keine Constraints verletzt werden, wird dieses Set von Variablen in einer Lösungsmatrix gespeichert. Danach wird das Backtracking fortgesetzt, um weitere Lösungen zu finden.
¶ Sichere Züge finden
In der Lösungsmatrix wird anschließend nach einem Feld gesucht, das in allen Lösungen denselben Wert besitzt. Wenn ein Feld in jeder möglichen Lösung den Wert 0 hat, gibt es keine Lösung, in der dieses Feld eine Mine ist. Das Feld kann daher sicher aufgedeckt werden. Umgekehrt gilt: Hat ein Feld in allen Lösungen den Wert 1, muss es eine Mine sein und kann entsprechend mit einer Flagge markiert werden.
Alle sicheren Züge werden daraufhin ausgeführt. Mit den neu gewonnenen Informationen wird ein neues CSP erstellt, um weitere Züge zu bestimmen. Im Optimalfall lässt sich dieser Prozess fortsetzen, bis das gesamte Spielfeld aufgedeckt ist und der Spieler gewonnen hat.
Allerdings gerät der Spieler häufig in Situationen, in denen keine sicheren Züge mehr gefunden werden können. In solchen Fällen bleibt nur die Möglichkeit, zu raten. [4:1]
¶ Optimiertes Raten
Wenn keine sicheren Züge mehr möglich sind, empfiehlt es sich, zunächst mögliche "Crapshots" zu lösen. C. Studholme definiert "Crapshots" als unlösbare Positionen, bei denen keine weiteren Informationen mehr gewonnen werden können. Es ist sinnvoll, diese Situationen zuerst zu klären, da ohnehin geraten werden muss. Dies sollte möglichst früh im Spiel geschehen, damit – falls ein falscher Zug gemacht wird – die nächste Runde schnell begonnen werden kann.

Beispiel für einen "Crapshot" [4:2]
Sind alle "Crapshots" behoben und weiterhin keine sicheren Felder auffindbar, wird das Feld gewählt, das die höchste Wahrscheinlichkeit hat, sicher zu sein. Hierfür wird erneut die Lösungsmatrix herangezogen. Unter der Annahme, dass alle gefundenen Lösungen gleich wahrscheinlich sind, wird das Feld aufgedeckt, das in den meisten Lösungen den Wert 0 hat, da bei diesem die Gefahr einer Mine am geringsten ist. Anschließend wird der Algorithmus erneut gestartet.
Felder, die mit hoher Wahrscheinlichkeit eine Mine (Wert 1) enthalten, werden für das Raten nicht in Betracht gezogen, da sie keine sicheren neuen Informationen liefern können.[4:3]
¶ Ergebnisse
Zur Analyse wurde der CSP-Algorithmus mit den zuvor betrachteten Algorithmen der Equation-Strategy und der SinglePoint-Strategy verglichen. Über 10.000 Simulationen hinweg wurden die Gewinnraten ermittelt, mit folgendem Ergebnis:
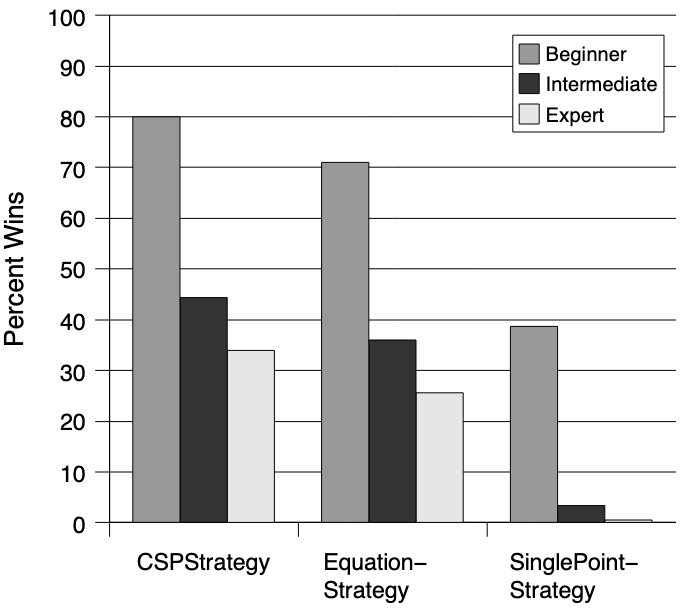
Gewinnraten mit sicherem erster Zug[4:4]
Die Ergebnisse zeigen, dass der CSP-Algorithmus auf der Beginner-Stufe etwa 80 % der Spiele gewinnen kann. Obwohl die Gewinnrate für die Intermediate-Stufe auf unter 50 % und für die Expert-Stufe auf knapp ein Drittel sinkt, schneidet der Algorithmus dennoch deutlich besser ab als die anderen beiden Strategien. Aufgrund der unlösbaren Situationen und des häufig notwendigen Ratens auf höheren Schwierigkeitsgraden – was sich insbesondere in der niedrigen Gewinnrate des SP-Algorithmus zeigt – ist es nachvollziehbar, dass eine wesentlich höhere Gewinnrate schwer zu erreichen ist.
Wie D. Baccera in seiner Arbeit anmerkte, erscheint das Backtracking in einem potenziell sehr großen Suchraum aufwendig. C. Studholme hat jedoch auch die Laufzeiten der Algorithmen analysiert. Dabei schnitt die CSP-Implementierung ebenfalls hervorragend ab, da sie oft mehrere Züge gleichzeitig ermitteln kann.[4:5]
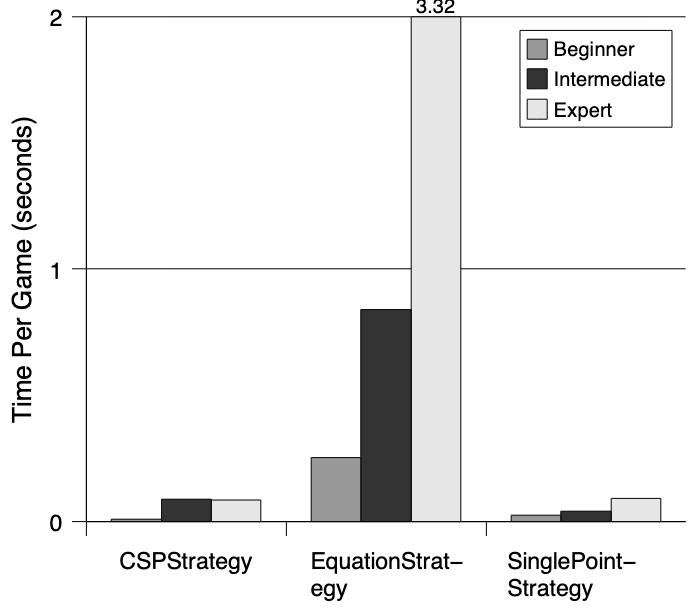
CPU Laufzeiten nach Schwierigkeitsgrad[4:6]
¶ Fazit
Die Darstellung von Minesweeper als CSP ist eine effektive Methode, um Gewinnraten und Effizienz zu verbessern. Aufgrund der vielen unklaren Informationen und der existierenden unlösbaren Stellungen bleibt jedoch eine hundertprozentige Lösung unmöglich.
¶ Referenzen
K. Pedersen, The complexity of Minesweeper and
strategies for game playing, Department of Computer Science at the University of Warwick, 2003-2004 ↩︎ ↩︎ ↩︎B. Kunz, Approaches to creating solvable Minesweeper instances and providing assistance during game playing using constraint programming, Tu Berlin, 2024 ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
D. Becerra, Algorithmic Approaches to Playing Minesweeper, Harvard College, 2015 ↩︎ ↩︎ ↩︎
C. Studholme, Minesweeper as a Constraint Satisfaction Problem,Department of Computer Science, University of Toronto, 2000 ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎