¶ Rubik's Cube
Der Rubik's Cube, auch Zauberwürfel genannt, ist ein 1974 von Ernő Rubik erfundenes und 1980 international popularisiertes Kombinatorikpuzzle.
¶ Allgemeines
Der Würfel besteht traditionellerweise aus 26 sichtbaren "Würfelchen", auch "Cubies" genannt. Jeder Cubie hat 1-3 sichtbare Farben (ein Eckstein hat 3, ein Kantenstein 2 und die mittleren Cubies jeder Fläche nur eine Farbe). In der Grundstellung sind alle Flächen einfarbig gefärbt. Ziel des Puzzles ist es, den Würfel durch Drehungen der Flächen zurück in die Grundstellung zu bringen, nachdem er durch zufällige Drehungen in eine Ausgangsposition zum Lösen gebracht wurde.
Rubik's Cube in Ausgangsstellung mit verdrehter außen liegender Fläche[1]
Physisch ist es möglich, sowohl eine der außen liegenden Flächen des Würfels, als auch die mittlere Schicht zu drehen. Letzteres kann allerdings auch als eine entsprechende Drehung der beiden äußeren Flächen betrachtet werden. Folglich können alle physisch möglichen Bewegungen des Würfels als eine Drehung einer äußeren Fläche, bzw. eine hintereinander folgende Kombination von zwei Drehungen beschrieben werden. Des Weiteren wird oft die sogenannte "half-turn metric" gewählt, um den Rubik's Cube formal zu beschreiben. Das bedeutet, dass eine Drehung einer Fläche des Würfels sowohl eine Drehung um 90°, als auch 180° sein kann. Unter dieser Notation ist nachgewiesen worden, dass "God's number", also die maximale Anzahl an Zügen die benötigt werden, um jede mögliche Ausgangsstellung des Würfels zu lösen, 20 ist.[2]

Ein Zauberwürfel in zufälliger Stellung mit verdrehter außen liegender Fläche[3]
In der Regel wird der mittlere Cubie jeder Fläche bei der theoretischen Betrachtung des Würfels als nicht beweglich beschrieben, da er nur eine Farbe hat und die Rotation der sichtbaren Fläche dieses Cubies somit den Zustand des Würfels nicht verändert. Damit gibt es formal nur 20 bewegliche Cubies, mit denen der Zustand des Würfels eindeutig beschrieben werden kann. Trotzdem ist die Anzahl möglicher Stellungen sehr groß: Betrachtet man alle durch zulässige Drehungen eines lösbaren physischen Würfels erreichbare Zustände, ergeben sich 43.252.003.274.489.856.000 Zustände.[4]
¶ Lösungsansätze
¶ Methoden für Menschen
Gängige Lösungsstrategien für Menschen basieren meist darauf, dass das Problem durch die Lösung von Teilproblemen vereinfacht wird, und somit die Komplexität des noch zu lösenden Teils verringert wird. Das wird oft mit Hilfe von kleinen Algorithmen gemacht die benutzt werden können, um bestimmte Stellungen des Würfels gezielt in andere Stellungen zu überführen. Beispielsweise kann zuerst eine vollständige Fläche des Würfels gelöst werden, die dann als oben liegende Fläche festgelegt wird, wonach ein bestimmter Algorithmus wiederholt angewandt werden kann, um die zweite Schicht zu lösen. Die letzte Schicht kann dann ebenfalls mit weiteren mehr oder wenig kurzen Algorithmen strategisch gelöst werden.[5]

Algorithmus zum gezielten Bilden eines einfarbigen Kreuzes auf der obersten Fläche eines ansonsten gelösten Würfels[6]
¶ Algorithmische Lösung mit IDA*
Solche Strategien sind zwar für Menschen geeignet, da simplere Methoden lediglich das Merken von wenigen, in der Regel bis zu etwa 10 Züge langen Algorithmen erfordern, allerdings wird der Würfel auf diese Art in fast allen Fällen nicht auf dem kürzesten Weg gelöst. Wie von Richard E. Korf 1997 gezeigt bietet allerdings der Iterative Deepening A* (IDA*) Algorithmus einen effektiven Weg, um optimale Lösungswege für den Rubik's Cube zu finden.[7]

Darstellung des Ablaufs einer A*-Suche. Alle eingefärbte Punkte in der Animation werden generiert und gespeichert, was bei Suchproblemen wie dem Rubik's Cube, die einen sehr hohen Verzweigungsgrad haben, zu Speicherproblemen führen kann.[8]
Die 1985 erstmals von Korf selbst eingeführte Abwandlung[9] des A*-Algorithmus[10][11] eignet sich für dieses Suchproblem, da A* zwar optimale Lösungen schnell finden kann, dafür jedoch exponentiellen Speicherbedarf hat, da bei der Suche alle generierten Knoten des Suchbaums gespeichert werden. Zur Umgehung dieses Problems kann Iterative Deepening als Zusatz zu A* verwendet werden. IDA* sucht schrittweise nach immer längeren Lösungen im Suchbereich und vermeidet es durch Schätzung des potenziellen Nutzens von Suchpfaden (und anschließendem Aussortieren von zu langen Pfaden), große Mengen irrelevanter Knoten bei der Suche zwischenzuspeichern.
¶ Heuristik
Für andere ähnliche Puzzle wird unter anderem eine dreidimensionale Form der Manhattan-Distanz verwendet. Bei dem Rubik's Cube würde hierbei für jeden Cubie einer zu bewertenden Stellung die minimale Anzahl an Zügen berechnet werden die benötigt werden, um den Cubie an die richtige Position zu bewegen und korrekt zu orientieren. Hierbei wird allerdings zum Beispiel nicht beachtet, wie sich die restlichen Cubies bei dieser Bewegung verändern. Zudem ist die erneute Berechnung von 20 Werten für jede neue Stellung bei diesem großen Suchbereich nicht zu vernachlässigend rechenaufwändig. Diese Heuristik ist also suboptimal.
Aufgrund der vielen Verzweigungen des Puzzles gibt es keine einfache generelle Regel mit der zuverlässig abgeschätzt werden kann, wie sehr die Bewegung eines bestimmten Cubies in seine Zielposition und -orientierung die Positionierung der restlichen Cubies positiv oder negativ mit Bezug auf den Zielzustand beeinflusst. Es gibt viele Wege einen Cubie in eine andere Position zu bringen, die ähnlich viele Züge benötigen, bei denen je nach Bewegung jedoch die Position vieler anderer Cubies mehr oder weniger negativ beeinflusst wird. Bei solchen Problemen können Pattern Databases hilfreich sein.
Pattern Databases können bei bestimmten kombinatorischen Problemen Abhilfe schaffen, da hier nach dem Brute-Force-Prinzip alle teilweisen Lösungen eines Problems bis zu einer gewissen Tiefe generiert werden und auf Basis dieses Wissens die weitere Suche vorgenommen wird. Die sich dadurch ergebende sehr genaue Bewertung der Teillösungen kann als Heuristik für einen geeigneten Suchalgorithmus verwendet werden. Eine Pattern Database ist also eine Ansammlung an Teillösungen eines Problems, bei der jeder Zustand des Suchbereichs in Verbindung mit einer partiellen Lösung gebracht werden kann, die eine Abschätzung des Wertes dieses Zustandes liefert.[12] Dadurch, dass diese Werte vor der Suche einmalig berechnet werden, und während der Suche nur noch ein Speicherzugriff pro Zustand erfolgen muss, wird auch die benötigte Berechnungszeit bei der Suche verkürzt.
Verwendet man bei der Anwendung von Pattern Databases auf IDA* zur Lösung des Rubik's Cube nur die Ecksteine des Würfels um den Wert eines Zustands abzuschätzen, müssen mit dem Brute-Force-Ansatz alle möglichen Kombinationen der Positionen und Orientierungen aller 8 Eck-Cubies generiert werden. Dies kann mit einer Breitensuche vom Zielzustand aus gemacht werden, bei der durch Ausprobieren aller möglichen Zugkombinationen vom gelösten Würfel aus ermittelt wird, wie viele Züge minimal benötigt werden, um vom Zielzustand in einen bestimmten Zustand mit einer bestimmten Kombination von Ecksteinen zu gelangen. Da die selbe Zugkombination einfach in umgekehrter Reihenfolge verwendet werden kann, um die gefundene Kombination von Ecksteinen zu lösen, ergibt diese Breitensuche eine Tabelle, in der für jede Kombination von Ecksteinen gespeichert wird, wie viele Züge minimal zum Lösen benötigt werden. Bei der Suche nach der optimalen Lösung eines Ausgangszustands mit IDA* entspricht also der Heuristikwert eines Zustands dem Eintrag in der Tabelle, der die minimale Zuganzahl für die aktuelle Anordnung der Eck-Cubies enthält.

Graphische Darstellung der Arbeitsfolge der Breitensuche. Die Zahlen der Knoten geben an, in welcher Reihenfolge die Knoten besucht werden[13]
Um diese Heuristik zu verbessern können noch die Kanten-Cubies mit einbezogen werden. Hierbei wird für die Kantensteine auf die gleiche Art und Weise eine Pattern Database erstellt, wie für die Ecksteine. Allerdings werden nicht alle Kanten-Cubies gleichzeitig betrachtet, da eine Aufzählung all ihrer Kombinationen erheblich mehr Rechenaufwand und Speicher benötigen würde, als schon für die Ecksteine, und somit potenziell den Vorteil durch besser informierte Entscheidungen bei der Suche zunichte machen würde. Zur Vereinfachung können die Kantensteine in zwei getrennten Gruppen betrachtet werden wodurch die Anzahl zu generierender Permutationen stark reduziert wird. Für beide Gruppen von Kanten-Cubies wird analog zu den Eck-Cubies eine Pattern Database erstellt, deren Werte bei der Suche mit IDA* als Heuristik verwendet werden können. Der Heuristikwert für einen Zustand des Rubik's Cube wird ermittelt, indem die Bewertung des aktuellen Zustands aus allen drei Tabellen genommen wird, und der höchste der drei Werte verwendet wird.
¶ Speicherbedarf
Die beschriebenen Pattern Databases benötigen für heutige Verhältnisse vernachlässige Mengen an Speicher. Die Tabelle für die Ecksteine verbraucht den meisten Speicherplatz: Die Anzahl der zu generierenden Kombinationen lässt sich berechnen als . Dies ergibt sich daraus, dass es 8 zu betrachtende Cubies gibt, jeder Cubie 3 verschiedene Orientierungen haben kann, und die Positionierung des letzten Cubies durch die anderen 7 festgelegt wird. Da die Zahl der benötigten Züge für die Ecksteine zwischen 0 und 11 liegt und die Zahl 11 binär als 1011 dargestellt wird, werden für die Speicherung eines Eintrags nur 4 Bits benötigt, was in der Summe einen Speicherbedarf von lediglich rund 44 Megabyte ergibt. Selbst wenn jede Zahl als 8- oder 16-Bit-Integer gespeichert würde, wie in modernen Anwendungen üblich, würde sich das auch nur auf einen Speicherbedarf von etwa 88 (bei 8-Bit-Integern) bzw. 176 Megabyte belaufen (bei 16-Bit-Integern).
Die beiden Pattern Databases für die Kantensteine enthalten jeweils Einträge. Da die maximale Anzahl benötigter Züge hier 10 beträgt, können die Einträge wieder mit 4 Bit Speicher dargestellt werden. Das ergibt einen Speicherbedarf von ca. 21 Megabyte, bei der Verwendung von 8-Bit-Integern knapp über 42 Megabyte, und bei 16-Bit-Integern auch nur etwas mehr als 85 Megabyte. Insgesamt können also alle drei Pattern Databases, die 1997 von Richard E. Korf verwendet wurden, in gerade einmal 82 Megabyte gespeichert werden. Selbst bei der Verwendung von heute gängigeren Formaten wie 16-Bit-Integern würden die Tabellen nur etwa 346 Megabyte verbrauchen, was auf modernen Systemen auch in der Regel leicht unterzubringen ist.
Korf verwendete bei der Erstellung des seines Papers zur Lösung des Rubik's Cube mit IDA*[7:1] die beiden getrennten Tabellen zu jeweils 6 Kantensteinen des Würfels als Teil der Heuristik, um Speicher zu sparen. Moderne Rechner haben um ein vielfaches mehr Leistung und Speicher, wodurch eine Betrachtung von mehr als nur 6 Kanten-Cubies in einer Pattern Database durchaus praktikabel wäre. Zum Vergleich: Herkömmliche PCs, die 1997 zum Zeitpunkt der Erscheinung von Korfs Paper verkauft wurden, hatten etwa 8 bis 32 Megabyte RAM[14], was betont, wie wichtig es für die Suche mit IDA* war, nicht zu viel Speicher zu verbrauchen, selbst wenn zur Berechnung für die Zeit extrem Leistungsfähige Rechner verwendet wurden.
¶ Ergebnisse
In einem praktischen Versuch erhielt Korf folgende Ergebnisse:
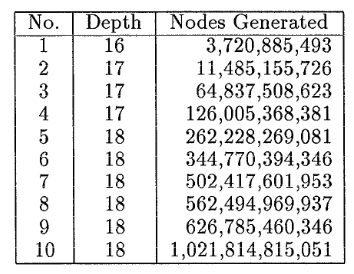
Länge der gefundenen optimalen Lösung jeder der 10 zufällig generierten Ausgangszustände des Rubik's Cube, als auch die Anzahl der bei der Suche generierten Knoten[7:2]
Es wurden zum Testen des Algorithmus 10 Ausgangszustände des Zauberwürfels generiert, indem 100 zufällige Züge auf einem gelösten Würfel ausgeführt wurden. Anschließend wurde mit IDA* in Verbindung mit den Pattern Databases für die Kanten- und Eck-Cubies verwendet, um diese Instanzen des Würfels zu lösen. Der verwendete Rechner (Sun UltraSparc Model 1) hatte einen Prozessor mit einem Kern und einer Taktfrequenz von bis zu 200 MHz.[15][16][17] Damit wurde für eine vollständige Suche mit einer Suchtiefe von 16 mit durchschnittlich 9,5 Milliarden generierten Knoten eine Berechnungszeit von unter 4 Stunden ermittelt, für Suchen mit Tiefe 17 und durchschnittlich 122 Milliarden generierten Knoten eine Zeit von etwa 2 Tagen und für eine Suchtiefe von 18 rund 4 Wochen ermittelt.
¶ Referenzen
https://commons.wikimedia.org/wiki/File:Rubik's_cube_2.svg ↩︎
https://www.speedcube.com.au/pages/how-to-solve-a-rubiks-cube ↩︎
Korf, Richard E. "Finding optimal solutions to Rubik's Cube using pattern databases." In AAAI/IAAI, pp. 700-705. 1997. PDF ↩︎ ↩︎ ↩︎
https://upload.wikimedia.org/wikipedia/commons/5/5d/Astar_progress_animation.gif ↩︎
Korf, Richard E. "Depth-first iterative-deepening: An optimal admissible tree search." Artificial intelligence 27, no. 1 (1985): 97-109. PDF ↩︎
Hart, Peter E., Nils J. Nilsson, and Bertram Raphael. "A formal basis for the heuristic determination of minimum cost paths." IEEE transactions on Systems Science and Cybernetics 4, no. 2 (1968): 100-107. IEEE ↩︎
Culberson, Joseph C., and Jonathan Schaeffer. "Pattern databases." Computational Intelligence 14, no. 3 (1998): 318-334. PDF ↩︎
https://commons.wikimedia.org/wiki/File:Breadth-First-Search-Algorithm.gif ↩︎
https://en.wikipedia.org/wiki/Sun_Ultra_series#Ultra_workstations_(1995–2001) ↩︎