¶ Beschreibung
Alpha-Beta-Pruning ist eine Optimierung des Minimax- Algorithmus, die die Anzahl der zu untersuchenden Zustände im Suchbaum verringert und so die Laufzeit reduziert. Das Verfahren erweitert den klassischen Algorithmus um zwei Parameter: α (Alpha) und β (Beta). Diese Parameter repräsentieren das sogenannte Suchfenster und definieren untere und obere Schranken für die Bewertung der Knoten:
-
α steht für den aktuell besten Minimax-Wert, den der maximierende Spieler (MAX) erreichen kann.
-
β steht für den aktuell besten Minimax-Wert, den der minimierende Spieler (MIN) erreichen kann.
Wenn während der Suche ein Spieler einen Wert findet, der außerhalb des aktuellen Suchfensters liegt (das heißt, wenn β ≤ α eintritt), bedeutet dies, dass der Gegner diesen Zug bei optimalem Spiel nicht wählen würde. Daher können alle verbleibenden Alternativen in diesem Zweig ignoriert werden. Dieser Prozess, bekannt als Cutoff, verringert die Anzahl der zu analysierenden Knoten und spart somit erheblich an Rechenzeit.
¶ Pseudocode
AlphaBeta (Knoten, Spieler, Alpha, Beta):
wenn Knoten ein Blatt ist:
gib den Wert des Knoten zurück
wenn Spieler == 1:
maxWert = -∞
für jeden Nachfolger des Knotens:
Wert = AlphaBeta(Nachfolger, -1, Alpha, Beta)
maxWert = max(maxWert, Wert)
Alpha = max(Alpha, maxWert)
wenn Beta <= Alpha:
breche ab
gib maxWert zurück
sonst:
minWert = ∞
für jeden Nachfolger des Knotens:
Wert = AlphaBeta(Nachfolger, 1, Alpha, Beta)
minWert = min(minWert, Wert)
Beta = min(Beta, minWert)
wenn Beta <= Alpha:
breche ab
gib minWert zurück
¶ Erläuterung
¶ Eingabe
Der Algorithmus erhält folgende Parameter:
- Knoten: Repräsentiert den aktuellen Spielzustand
- Spieler: Gibt an, welcher Spieler am Zug ist (1 für den Maximierer und -1 für den Minimierer)
- Alpha: Der beste Wert, den der Maximierer entlang des aktuellen Pfades garantiert erreichen kann
- Beta: Der beste Wert, den der Minimierer entlang des aktuellen Pfades garantiert erreichen kann
¶ Abbruchbedingung
Wenn der aktuelle Knoten ein Blatt ist (entweder aufgrund einer festgelegten Suchtiefe oder weil keine Nachfolger mehr vorhanden sind), wird dessen Wert zurückgegeben. Dieser Wert stammt aus einer heuristischen Funktion, die den Spielzustand bewertet.
¶ Maximierer
- Initialisierung: Der maximale Wert (maxWert) wird auf -∞ gesetzt
- Iteration: Für jeden Nachfolger ruft der Algorithmus rekursiv AlphaBeta auf, wobei der Spieler zu -1 wechselt
- Maximierung: Der maxWert wird aktualisiert, um den höchsten Wert aller Nachfolger zu finden
- Alpha-Aktualisierung: Alpha wird aktualisiert, um den besten Wert für den Maximierer entlang des Pfades widerzuspiegeln
- Pruning: Wenn Beta <= Alpha, wird der Rest der Nachfolger nicht mehr untersucht, da der Minimierer diesen Pfad ohnehin nicht wählen würde
- Rückgabe: Am Ende wird der maximale Wert (maxWert) zurückgegeben
¶ Minimierer
- Initialisierung: Der minimale Wert (minWert) wird auf ∞ gesetzt
- Iteration: Für jeden Nachfolger ruft der Algorithmus rekursiv AlphaBeta auf, wobei der Spieler zu 1 wechselt
- Minimierung: Der minWert wird aktualisiert, um den niedrigsten Wert aller Nachfolger zu finden
- Beta-Aktualisierung: Beta wird aktualisiert, um den besten Wert für den Minimierer entlang des Pfades widerzuspiegeln
- Pruning: Gleich wie beim Maximierer
- Rückgabe: Am Ende wird der minimale Wert (minWert) zurückgegeben
¶ Ergebnis
Die Lösung des Spielbaumes ist der Minimax-Wert der Wurzel. Dieser gibt an, welcher Wert erzielt wird, wenn beide Spieler stets die bestmöglichen Züge wählen.
¶ Beispiel
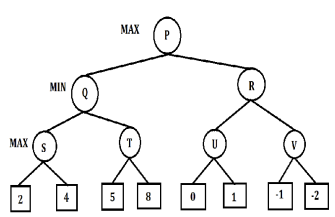
Betrachten wir folgendes Beispiel von Nasa et al. [1]. Zu Beginn hat Alpha den Wert minus unendlich und Beta den Wert plus unendlich. Der erste aufgerufene Knoten ist P. An P versucht der Maximierer, das Maximum zwischen Q und R auszuwählen. In diesem Fall wird zuerst Q von P aufgerufen, es wäre jedoch ebenso möglich, R zuerst aufzurufen.
Am Knoten Q versucht der Minimierer, das Minimum zwischen S und T zu bestimmen, weshalb S als erstes aufgerufen wird. Bei S liefert das linke Kind, ein Blattknoten, den Wert 2 zurück. Der aktualisierte Wert von Alpha an S ist das Maximum aus minus unendlich und 2, also 2. Um zu entscheiden, ob das rechte Kind untersucht werden sollte, wird die Bedingung überprüft, ob Beta kleiner oder gleich Alpha ist. Diese Bedingung ist nicht erfüllt, da Beta plus unendlich und Alpha 2 ist. Daher wird der Baum weiter durchsucht, und S untersucht sein rechtes Kind, das den Wert 4 zurückgibt. Nun ist Alpha an S das Maximum aus 2 und 4, also 4. Der Wert von S beträgt somit schließlich 4, und dieser wird an den Elternknoten Q zurückgegeben.
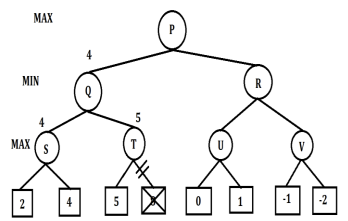
An Q wird Beta auf das Minimum aus plus unendlich und 4 gesetzt, also 4. Der Minimierer hat nun garantiert einen Wert von maximal 4. Q ruft sein rechtes Kind T auf, um zu überprüfen, ob ein Wert kleiner als 4 möglich ist. Bei T sind die Werte von Alpha und Beta nicht mehr minus unendlich und plus unendlich, sondern minus unendlich und 4, da Beta an Q aktualisiert wurde und dieser Wert an T weitergegeben wird.
T untersucht sein linkes Kind, das den Wert 5 liefert. An T ist Alpha das Maximum aus minus unendlich und 5, also 5. Da Beta gleich 4 und Alpha gleich 5 ist, erfüllt die Bedingung Beta ≤ Alpha. Daher muss das rechte Kind von T nicht weiter untersucht werden, auch wenn es einen höheren Wert als 5 enthält. Der rechte Zweig von T, der den Wert 8 speichert, wird somit abgeschnitten (pruned). T gibt den Wert 5 an Q zurück. Es spielt keine Rolle, welchen Wert das rechte Kind von T enthält, da der Minimierer an Q garantiert einen Wert von 4 oder weniger erreichen kann.
Dieser Prozess zeigt, wie Alpha-Beta-Suche unnötige Berechnungen vermeidet. Der Wert 5 von T wird an Q zurückgegeben. An Q wird Beta auf das Minimum aus 4 und 5 gesetzt, also 4. Somit speichert Q den Wert 4 und gibt ihn an P zurück.
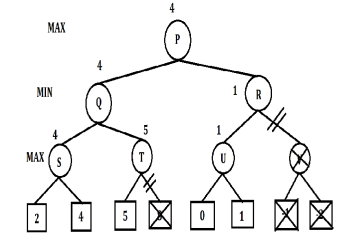
An P wird Alpha auf das Maximum aus minus unendlich und 4 gesetzt, also 4. Der Maximierer hat nun garantiert einen Wert von mindestens 4. P ruft dann sein rechtes Kind R auf, um zu prüfen, ob ein Wert größer als 4 erreicht werden kann. An R sind Alpha gleich 4 und Beta gleich plus unendlich. R untersucht sein linkes Kind U.
An U sind Alpha gleich 4 und Beta gleich plus unendlich. Das linke Kind von U liefert den Wert 0 zurück, sodass Alpha gleich dem Maximum aus 4 und 0 ist, also weiterhin 4. Das rechte Kind von U liefert den Wert 1, womit der beste Wert an U 1 ist, Alpha jedoch 4 bleibt. U gibt 1 an R zurück.
An R wird Beta auf das Minimum aus plus unendlich und 1 gesetzt, also 1. Die Bedingung Beta ≤ Alpha wird erfüllt, da Beta 1 und Alpha 4 ist. Daher wird der gesamte Unterbaum von V abgeschnitten, da keine weiteren Werte untersucht werden müssen. Der Minimierer an R ist auf einen Wert von 1 oder weniger beschränkt, während der Maximierer bereits einen Wert von 4 garantiert hat, indem er den linken Zweig von P (Knoten Q) wählt.
Der Wert 1 von R wird an P zurückgegeben. Der beste Wert an P ist das Maximum aus 4 und 1, also 4. Der optimale Wert, den der Maximierer erreichen kann, beträgt somit 4. Dies zeigt, wie der Algorithmus durch Alpha-Beta-Pruning die Anzahl der Berechnungen reduziert, indem ganze Teilbäume übersprungen werden.
¶ Negamax
Um den Algorithmus zu vereinfachen, kann die Negamax-Darstellung genutzt werden, bei der nur eine einzige Funktion für beide Spieler implementiert wird. Hierbei werden die Werte von α und β in jeder Schicht vertauscht und negiert, um die Perspektive des minimierenden bzw. maximierenden Spielers zu wechseln.
AlphaBetaNegamax(Knoten, Alpha, Beta):
wenn der Knoten ein Blatt ist:
gib den Wert des Knotens zurück
maxWert = -∞
für jeden Nachfolger des Knotens:
Wert = -AlphaBetaNegamax(Nachfolger, -Beta, -Alpha)
maxWert = max(maxWert, Wert)
Alpha = max(Alpha, Wert)
wenn Alpha >= Beta:
breche ab
gib maxWert zurück
¶ Weitere Optimierungen
¶ Anpassung des Suchfensters
Die Alpha-Beta-Suche kann durch Anpassung des Suchfensters für spezielle Anwendungsfälle optimiert werden. Ein kleineres Suchfenster, z. B. mit und , führt zu mehr Cutoffs und somit zu einer besseren Laufzeit. Allerdings liefert es nicht den exakten Minimax-Wert, sondern nur eine grobe Einschätzung:
- : Sieg für MIN,
- : Sieg für MAX,
- : Unentschieden.
Die extremste Form dieser Optimierung ist die Nullfenstersuche, bei der gesetzt wird. Diese Methode liefert lediglich eine obere oder untere Schranke für den Minimax-Wert, ermöglicht jedoch maximale Effizienz[2].
¶ Zugsortierung
Durch eine geschickte Reihenfolge bei der Untersuchung von Zügen kann die Alpha-Beta-Suche erheblich beschleunigt werden. Die meisten Cutoffs treten auf, wenn der optimale Pfad (Principal Variation) früh gefunden wird, da weniger erfolgversprechende Züge dadurch schnell ausgeschlossen werden können. Werden hingegen schlechte Züge zuerst geprüft, gibt es kaum Cutoffs, was die Suche unnötig verlängert.
Um gute Züge frühzeitig zu erkennen, müssen diese sinnvoll priorisiert werden. Bei Spielen wie Vier Gewinnt kann dies einfach durch Sortieren der Züge nach ihrer Nähe zur mittleren Spalte geschehen, da zentrale Spielsteine strategisch wertvoller sind. Diese statische Sortierung ist effizient und vermeidet zusätzlichen Rechenaufwand während der Suche[2:1].
¶ Transpositionstabelle
Oft untersucht die Alpha-Beta-Suche Positionen, die bereits untersucht wurden. Diese kann man in einer Transpositionstabelle speichern.
Eine Transpositionstabelle ist ein Cache von zuvor gesehenen Positionen und den damit verbundenen Bewertungen in einem Spielbaum. Wenn eine Position über eine andere Zugsequenz wieder auftaucht, wird der Wert der Position aus der Tabelle abgerufen, wodurch eine erneute Suche im Spielbaum unterhalb dieser Position vermieden wird. Transpositionstabellen sind insbesondere bei perfekten Informationsspielen nützlich (bei denen der gesamte Zustand des Spiels jederzeit allen Spielern bekannt ist), wie z.B. Dots And Boxes. Die Nutzung von Transpositionstabellen ist im Wesentlichen eine Abspeicherung, die auf die Baum-Suche angewendet wird, und stellt eine Form der dynamischen Programmierung[3] dar.
Transpositionstabellen werden typischerweise als Hash-Tabellen implementiert, wobei der aktuelle Spielzustand als Hash-Index verwendet wird. Da die Anzahl der möglichen Positionen, die in einem Spielbaum vorkommen können, sehr groß sein kann, werden Hashing-Methoden wie Zobrist-Hashing verwendet, um Kollisionen zu vermeiden und den Speicher effizient zu nutzen[2:2].
¶ Beispiele für Ersetzungsmethoden
- Deep: Behält die Spielposition mit dem tiefsten Teilbaum.
- New: Ersetzt immer die Spielposition.
- Old: Ersetzt nie die Spielposition.
- Big: Behält die Spielposition mit dem größten Teilbaum (Anzahl der Knoten).
Zudem gibt es auch weitere Methoden, bei welchen 2 Spielpositionen pro Hash gespeichert werden. Diese werden meist zusammen mit einer der vier oben genannten Methoden verwendet.[4]
¶ Laufzeit
Die Anzahl der abgeschnittenen Zweige durch Alpha-Beta-Pruning hängt von der Reihenfolge der Werte ab. Im schlechtesten Fall befinden sich die besten Werte für den maximierenden und minimierenden Spieler am Ende des Baumes (rechts), sodass Alpha-Beta-Pruning wie eine normale Minimax-Suche arbeitet und alle Knoten durchsucht. In diesem Fall liegt die Zeitkomplexität bei [5].
Im optimalen Fall, bei dem die besten Werte immer zuerst (links) geprüft werden, reduziert sich die Zeitkomplexität auf . Dies liegt daran, dass zwar alle Züge des ersten Spielers untersucht werden müssen, jedoch pro Zug nur der beste Gegenzug des zweiten Spielers betrachtet wird, wodurch jede zweite Ebene übersprungen wird[5:1].
In der Praxis liegt die Werte-Reihenfolge meist zwischen dem schlechtesten und dem idealen Fall. Dennoch untersucht Alpha-Beta-Pruning, selbst ohne ideale Reihenfolge, wesentlich weniger Knoten als eine einfache Minimax-Suche. Dies ermöglicht es, mit Alpha-Beta-Pruning tiefere Ebenen des Spielbaums zu durchsuchen als mit der Standard-Minimax-Suche.
¶ Referenzen
Anmerkung: Diese Seite wurde von Marin Dvojkovic verfasst (bis auf Transpositionstabellen ab:"Transpositionstabellen werden typischerweise als Hash-Tabellen implementiert..." . Weitere Änderungen von anderen Personen an diesem Artikel sind nicht mit dem Verfasser abgesprochen.
¶ Abbildungen
Pseudocode 1 übersetzt aus: Carl Felstiner. 2019. Alpha-beta pruning. [6]
Pseudocode 2 übersetzt aus: Yassin Liese. 2024. Entwicklung eines Frameworks zur systematischen Evaluierung und Optimierung Minimax-basierter Suchstrategien anhand des Spiels Vier-Gewinnt. [5:2]
Abbildung 1 aus: Rijul Nasa, Rishabh Didwania, Shubhranil Maji, and Vipul Kumar. 2018. Alpha-beta pruning in mini-max algorithm–an optimized approach for a connect-4 game.[1:1]
Abbildung 1 aus: Rijul Nasa, Rishabh Didwania, Shubhranil Maji, and Vipul Kumar. 2018. Alpha-beta pruning in mini-max algorithm–an optimized approach for a connect-4 game.[1:2]
Abbildung 1 aus: Rijul Nasa, Rishabh Didwania, Shubhranil Maji, and Vipul Kumar. 2018. Alpha-beta pruning in mini-max algorithm–an optimized approach for a connect-4 game.[1:3]
¶ Textquellen
Rijul Nasa, Rishabh Didwania, Shubhranil Maji, and Vipul Kumar. 2018. Alpha-beta pruning in mini-max algorithm–an optimized approach for a connect-4 game. Int. Res. J. Eng. Technol 5, (2018), 1637–1641. ↩︎ ↩︎ ↩︎ ↩︎
Yassin Liese. 2024. Entwicklung eines Frameworks zur systematischen Evaluierung und Optimierung Minimax-basierter Suchstrategien anhand des Spiels Vier-Gewinnt. Technische Universität Berlin, Berlin. Retrieved January 16, 2025 from https://doc.neuro.tu-berlin.de/bachelor/2024-BA-YassinLiese.pdf ↩︎ ↩︎ ↩︎
Dynamische Programmierung. Wikipedia. Retrieved January 20, 2025 from https://de.wikipedia.org/w/index.php?title=Dynamische_Programmierung&oldid=247978530 ↩︎
Breuker, Dennis M., et al. “Solving Domineering.” Theoretical Computer Science, vol. 230, no. 1–2, 2000, pp. 195–206, pdf. ↩︎
Abdoul Wahab Touré. 2023. Evaluation of the Use of Minimax Search in Connect-4 —How Does the Minimax Search Algorithm Perform in Connect-4 with Increasing Grid Sizes? AM 14, 06 (2023), 419–427. https://doi.org/10.4236/am.2023.146025 ↩︎ ↩︎ ↩︎
Carl Felstiner. 2019. Alpha-beta pruning. Whitman College (2019). Retrieved January 16, 2025 from https://www.whitman.edu/documents/Academics/Mathematics/2019/Felstiner-Guichard.pdf ↩︎