¶ Allgemein
Vier gewinnt ist ein strategisches Zwei-Personen-Spiel, bei dem es darum geht, als Erster vier eigene Spielsteine in einer Reihe zu platzieren. Das Spiel wurde von Howard Wexler unter Mitwirkung von Ned Strongin entwickelt, 1973 von der Strongin & Wexler Corp. an Milton Bradley (MB Spiele) lizenziert und 1974 veröffentlicht[1].
Es handelt sich um ein Nullsummenspiel[2], was bedeutet, dass der Gewinn eines Spielers immer dem Verlust des anderen Spielers entspricht – ein Prinzip, das in der Spieltheorie häufig verwendet wird. Ein Beispiel für ein nicht-Nullsummenspiel wäre Lotto.
Außerdem ist Vier Gewinnt ein Spiel mit perfekter Information. Ein Spiel verfügt über perfekte Information, wenn jedem Spieler bei jeder Entscheidung der gesamte bisherige Spielverlauf, einschließlich der vorherigen Züge aller Spieler bekannt ist.[3]
¶ Spielablauf und Regeln

Das Spiel wird auf einem senkrecht stehenden, hohlen Spielfeld gespielt. Es besteht aus sieben senkrechten Spalten und sechs waagerechten Reihen. Jeder Spieler hat 21 Spielsteine in einer eigenen Farbe, meistens rot oder gelb.
Die Spieler werfen abwechselnd ihre Spielsteine ein. Wird ein Stein in eine Spalte geworfen, belegt er den untersten freien Platz in dieser Spalte.
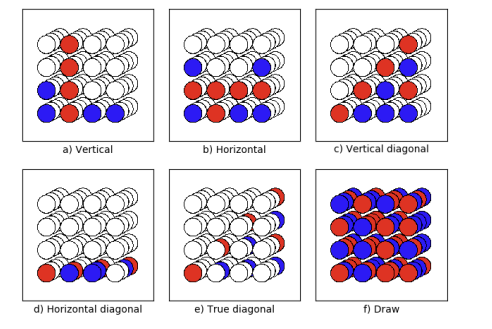
Das Ziel des Spiels ist es, vier oder mehr eigene Spielsteine in einer waagerechten, senkrechten oder diagonalen Linie zu platzieren. Ist das Spielfeld vollständig gefüllt, ohne dass eine Viererlinie gebildet wurde, endet das Spiel unentschieden.
¶ Beispiele



¶ Varianten des Spiels
¶ N x N Feld
Auf verschiedenen Spiele-Servern wird Vier Gewinnt häufig auf einem 8 × 8 Spielfeld gespielt, da das klassische 7 × 6 Spielfeld vollständig gelöst ist[1:1]. Die erhöhte Spielfeldgröße steigert die Komplexität des Spiels erheblich, was das Schummeln mit Solvern erschwert, da die Anzahl der möglichen Spielzustände und der strategischen Entscheidungen exponentiell zunimmt.
¶ 3D Vier Gewinnt
Eine weitere Variante von Vier Gewinnt ist 3D Vier Gewinnt, das im Unterschied zur klassischen Version in drei Dimensionen gespielt wird. Statt auf einem flachen 7 × 6-Brett spielen die Spieler auf einem 4 × 4 × 4-Würfel, der 16 vertikale Spalten enthält. Ziel ist es, vier Spielsteine der eigenen Farbe in einer geraden Linie anzuordnen – diese Linie kann sowohl in einer Ebene als auch über mehrere Ebenen hinweg verlaufen. Die zusätzliche Dimension erweitert die strategischen Möglichkeiten und macht das Spiel komplexer im Vergleich zur klassischen Variante[4].
¶ PopOut
Eine andere Variante ist PopOut, das auf einem klassischen 7x6-Brett gespielt wird, aber mit einer wichtigen Änderung: Spieler können neben dem Abwerfen eines neuen Steins auch bestehende Steine aus dem unteren Bereich einer Spalte entfernen. Diese Pop-Bewegung fügt eine neue strategische Dimension hinzu, da Spieler ihre Züge anpassen und auch die des Gegners beeinflussen können.[1:2]
¶ Komplexität
Obwohl Vier Gewinnt ein relativ einfach zu spielendes Spiel ist, ist eine Brute-Force-Lösung äußerst komplex, da es eine enorme Menge an möglichen Spielzuständen gibt. Die Anzahl dieser Zustände lässt sich aus den Spielfeldparametern ableiten:
Formelbestandteile
Die maximale Anzahl an möglichen Spielzuständen ergibt sich als:
Einsetzen der Werte:
Dies ist jedoch nur eine theoretische Obergrenze. Viele dieser Spielzustände sind in der Praxis nicht erreichbar, da das Spiel durch einen Gewinn frühzeitig endet oder das Spielfeld nicht vollständig gefüllt wird. Die tatsächliche Anzahl der legalen Spielzustände beträgt etwa 4,5 Billionen [5].
Vier Gewinnt wurde sowohl von Allis [6] als auch von Allen [7] im Jahr 1988 vollständig gelöst. Beide Forscher kamen zu dem gleichen Ergebnis: Bei optimalem Spiel gewinnt der beginnende Spieler, sofern er seinen ersten Spielstein in die mittlere Spalte einwirft. Wählt er hingegen eine der beiden direkt angrenzenden Spalten, endet das Spiel in einem Unentschieden, während alle anderen Eröffnungszüge zu einem Sieg für den Gegner führen.
¶ Algorithmische Lösung
¶ Minimax
Der Minimax-Algorithmus wird oft verwendet, um optimale Züge im Spiel Vier Gewinnt zu berechnen. In einem Spielbaum, der alle möglichen Züge abbildet, bewertet der Minimax-Algorithmus die Spielzustände, indem er den maximalen Wert für den Maximierer und den minimalen Wert für den Minimierer berechnet. Dabei wird angenommen, dass beide Spieler stets den besten Zug wählen. Der Algorithmus wird rekursiv angewendet und gibt den optimalen Zug des Spielers an, basierend auf den besten Antworten des Gegners.
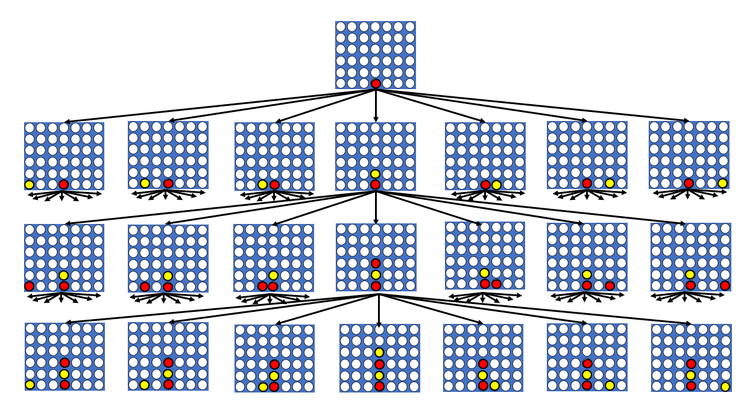
Für detailliertere Informationen und einen tieferen Einblick in den Minimax-Algorithmus sowie die damit verbundenen Optimierungen, wird auf den separaten Artikel über Minimax verwiesen.
Obwohl der Minimax-Algorithmus eine nützliche Methode für Vier Gewinnt darstellt, ist er in seiner einfachen Form ineffizient, da er die Anzahl der möglichen Züge exponentiell steigen lässt. Daher werden Optimierungen wie Alpha-Beta Pruning verwendet, um unnötige Berechnungen zu vermeiden und die Laufzeit zu verkürzen.
¶ Evaluation eines Spielzugs
Beim Minimax-Algorithmus erfolgt die Auswahl der Züge auf Basis ihrer Bewertungen, die durch eine heuristische Bewertungsfunktion bestimmt werden. Die Bewertungsfunktionen sind spielspezifisch und können angepasst werden. Im Folgenden sieht man eine einfache Bewertungsfunktion für Connect-4.[5:1]
Diese Funktion weist allen Chip-Gruppen ein Gewicht zu, abhängig davon, wie viele Chips in einer Gruppe ausgerichtet sind. Eine Chip-Gruppe besteht aus zwei oder mehr Chips derselben Farbe, die vertikal, horizontal oder diagonal ausgerichtet sind.
Der von der Bewertungsfunktion zurückgegebene Wert ist die Summe aller Gewichtungen des maximierenden Spielers minus der Summe aller Gewichtungen des minimierenden Spielers.
Formelbestandteile
| Number of tokens lined up | Weight (w) |
|---|---|
| 2 | 1 |
| 3 | 10 |
| 4 | 1000 |
Dieses Beispiel zur Bewertung eines Spielzugs war einfach und veranschaulicht das grundlegende Konzept. Im Artikel von Kang et al.[8] wird auf weitere komplexere Heuristiken eingegangen, die die Funktionalität des Minimax-Algorithmus bei der Analyse von Connect-4-Spielzügen verbessern.
Zur Bewertung der aktuellen Spielsituation verwendet die im folgenden gezeigte Heuristik eine Methode, bei der sie verschiedene Merkmale auf dem Spielfeld sucht und diesen jeweils entsprechende Werte zuweist. Am Ende gibt die Heuristik die Summe aller Werte der erkannten Merkmale auf dem Spielfeld zurück.
Die Heuristik sucht nach vier verschiedenen Merkmalen auf dem Spielfeld, die in Tabelle 1 aufgeführt sind. Die für diese vier Merkmale vergebenen Werte, werden in Tabelle 2 dargestellt.
| Merkmal | Beschreibung |
|---|---|
| Merkmal 1 | Absoluter Gewinn: Vier Spielfiguren sind horizontal, vertikal oder diagonal miteinander verbunden |
| Merkmal 2 | Drei verbundene Spielfiguren: Drei Spielfiguren sind horizontal, vertikal oder diagonal miteinander verbunden |
| Merkmal 3 | Zwei verbundene Spielfiguren: Zwei Spielfiguren sind horizontal, vertikal oder diagonal miteinander verbunden |
| Merkmal 4 | Einzelne Spielfigur: Eine Spielfigur, die nicht mit einer anderen gleichen Spielfigur horizontal, vertikal oder diagonal verbunden ist |
| Merkmal | Beschreibung | Wert |
|---|---|---|
| Merkmal 1 | Unendlich | |
| Merkmal 2 | Ein Zug kann in beiden benachbarten Spalten gemacht werden. | Unendlich |
| Ein Zug kann nur in einer benachbarten Spalte gemacht werden. | 900.000 | |
| Eine gleiche Spielfigur ist einen Platz entfernt von zwei verbundenen Spielfiguren. | 900.000 | |
| Merkmal 3 | Ein Zug kann in beiden benachbarten Spalten gemacht werden. | 50.000 |
| Ein Zug kann nur in einer der benachbarten Spalten gemacht werden (der Wert hängt von der Anzahl der verfügbaren Felder ab). | ||
| Anzahl der verfügbaren Felder: 5 | 40.000 | |
| Anzahl der verfügbaren Felder: 4 | 30.000 | |
| Anzahl der verfügbaren Felder: 3 | 20.000 | |
| Anzahl der verfügbaren Felder: 2 | 10.000 | |
| Merkmal 4 | In Spalte 4 | 200 |
| In Spalte 1 oder 7 | 40 | |
| In Spalte 2 oder 6 | 70 | |
| In Spalte 3 oder | 120 |
In der Funktion werden diese Merkmale auf dem Spielfeld erkannt und ihre Werte summiert. Wenn ein Merkmal für den Spieler vorteilhaft ist, wird ein positiver Wert vergeben, andernfalls ein negativer.
Die andere in dem Artikel beschriebene Heuristik unterscheidet sich von der ersten, indem sie nicht nach bestimmten Merkmalen auf dem Spielfeld sucht. Stattdessen bewertet sie jedes einzelne Quadrat auf dem Spielfeld und weist ihm je nach Relevanz unterschiedliche Werte zu. Ein Quadrat, das vielversprechender ist, erhält einen höheren Wert. Die Werte basieren auf der Nähe zum zentralen Bereich des Spielfelds, da dieser eine größere Möglichkeit zur Bildung von vier verbundenen Steinen in horizontaler, vertikaler und diagonaler Ausrichtung bietet. Felder in der Nähe der Mitte haben daher einen höheren Wert, während Felder am Rand einen niedrigeren Wert haben, da sie weniger Expansionsmöglichkeiten bieten. Diese Heuristik bewertet also, wie nützlich jedes Quadrat für den Gewinn des Spiels ist, und unterstützt die Entscheidungsfindung der Strategie.
¶ Alpha-Beta Pruning
Alpha-Beta-Pruning ist eine bedeutende Optimierung des Minimax-Algorithmus, die dazu dient, die Anzahl der zu prüfenden Zustände im Suchbaum zu reduzieren und dadurch die Laufzeit erheblich zu verbessern. Dies wird erreicht, indem zwei zusätzliche Parameter, α (Alpha) und β (Beta), eingeführt werden. Diese Parameter stellen die untere und obere Schranke für die Bewertung der Knoten dar:
Neue Variablen
Durch das Setzen dieser Schranken ist der Algorithmus in der Lage, ganze Teilbäume zu ignorieren, wenn sie nicht weiter untersucht werden müssen, weil der Wert des Knotens bereits außerhalb des aktuellen Suchfensters liegt. Dieser Cutoff spart an Rechenzeit und erhöht die Effizienz der Suche.
Für genauere Details zur Funktionsweise und Anwendung von Alpha-Beta-Pruning im Zusammenhang mit dem Minimax-Algorithmus, siehe den verlinkten Abschnitt über Alpha-Beta Pruning.
¶ Laufzeitverbesserung durch Alpha-Beta Pruning
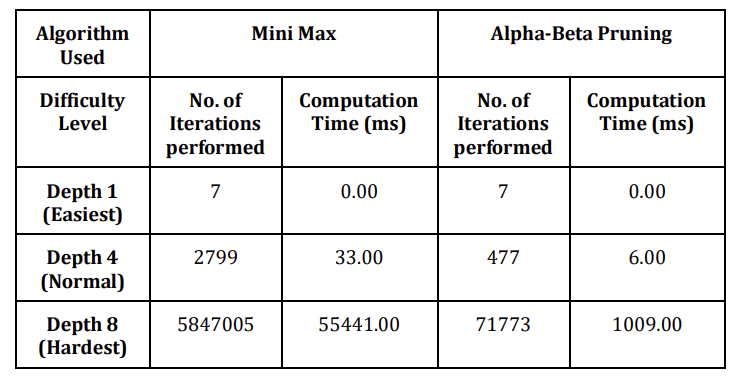
Man kann erkennen, dass das Alpha Beta Pruning die Laufzeit deutlich verbessert, und dass der Faktor der Zeitverbesserung mit der Tiefe des Baums steigt. Während die Variante mit Alpha-Beta Pruning bei einer Tiefe von 4 fast 6 mal so effizient ist, ist sie bei einer Tiefe von 8 schon knapp 55 mal so schnell[9].
Im Idealfall hat der Minimax Algorithmus eine Laufzeit von wobei b der Verzweigungsgrad und m die Tiefe des Baums ist. Im Gegensatz dazu kann man mit Alpha-Beta Pruning im besten Fall eine Laufzeit von erreichen.
Der optimale Fall ist dann erreicht, wenn die Züge in einer Reihenfolge überprüft werden, bei der immer der bestmögliche Zug zuerst kommt. Dies maximiert die Effektivität des Alpha-Beta-Prunings und minimiert die Anzahl der zu prüfenden Knoten im Entscheidungsbaum.[5:2]
Die Ergebnisse aus dem Experiment sind jedoch vergleichsweise sehr langsam und obwohl die Alpha-Beta-Suche häufig verwendet wird, ist sie nicht die beste Lösung und weitere Optimierungen sind notwendig.
¶ Weitere Optimierungen
In der Bachelorarbeit von Yassin Liese[10] wird auf weitere Optimierungen wie die Principal-Variation-Suche (PVS), NegaC* und MTD(f) eingegangen. Mit den Optimierungen ist es ihm gelungen, das Spiel in nur 3 Minuten zu lösen. Aufgrund des Umfangs und der Komplexität der Thematik wird an dieser Stelle nur grundlegend auf die 3 Algorithmen eingangen.
¶ Principal-Variation-Suche (PVS)
Die Principal-Variation-Suche (PVS) ist eine Optimierung des Alpha-Beta-Algorithmus, die darauf abzielt, die Principal-Variation (die wahrscheinlich beste Zugfolge) effizient zu identifizieren. Sie nimmt an, dass der erste Kindknoten zur Principal-Variation gehört und evaluiert ihn vollständig. Für alle anderen Geschwisterknoten werden zunächst Nullfenstersuchen mit einem engen Suchfenster [𝛼,𝛼+1] durchgeführt, um sie effizient auszuschließen. Nur wenn ein Geschwisterknoten eine bessere Bewertung als der erste Kindknoten erzielt, wird auch für ihn eine vollständige Suche durchgeführt. Die Effizienz von PVS hängt stark von der Qualität der Zugsortierung ab, da eine gute Sortierung früh viele Cutoffs erzeugt.
PVS (Knoten, α, β):
wenn Knoten ein Endknoten ist:
gib die Bewertung des Knotens zurück
Wert = −∞
ersterZug = wahr
für jeden Nachfolger des Knotens:
wenn ersterZug:
Punktzahl = −PVS(Nachfolger, −β, −α)
sonst:
Punktzahl = −PVS(Nachfolger, −α − 1, −α)
wenn Punktzahl > α:
Punktzahl = −PVS(Nachfolger, −β, −α)
wenn Punktzahl ≥ β:
gib Punktzahl zurück
ersterZug = falsch
wenn Punktzahl > Wert:
Wert = Punktzahl
wenn Punktzahl > α:
α = Punktzahl
gib Wert zurück
¶ MTD(f)
MTD(f) ist ein auf der Alpha-Beta-Suche basierender Algorithmus, der ausschließlich mit Nullfenstersuchen arbeitet, um den tatsächlichen Minimax-Wert iterativ zu bestimmen. Der Algorithmus startet mit einer anfänglichen Schätzung f die als erste Näherung des Ergebnisses dient. Eine Variable g initial auf f gesetzt, wird während der Iterationen angepasst, indem jeweils Nullfenstersuchen um den aktuellen Wert von g durchgeführt werden. Dabei wird das Suchfenster durch zwei Schranken, min und max, begrenzt. Je nachdem, ob das Ergebnis der Nullfenstersuche eine obere oder untere Schranke darstellt, wird das Suchfenster entsprechend angepasst. Der Algorithmus terminiert, sobald min und max denselben Wert annehmen, der dann den tatsächlichen Minimax-Wert darstellt.
MTD(f) (Knoten, f):
g = f
min = −∞
max = ∞
wiederhole:
wenn g = min:
β = g + 1
sonst:
β = g
g = alphaBetaMitSpeicher(Knoten, β − 1, β)
wenn g < β:
max = g
sonst:
min = g
bis min >= max
gib g zurück
¶ NegaC*
Die NegaC*-Suche ist eine Variante der Negamax-Suche, die den tatsächlichen Minimax-Wert durch mehrere Nullfenstersuchen iterativ bestimmt. Im Gegensatz zu MTD(f) wird das Suchfenster dabei nicht um den Wert der vorherigen Iteration gelegt, sondern bisektionsartig verkleinert.
Zu jedem Schritt wird der Mittelwert des aktuellen Suchfensters gebildet, und eine Nullfenstersuche überprüft, ob der tatsächliche Minimax-Wert größer oder kleiner gleich diesem Mittelwert ist. Das Ergebnis der Nullfenstersuche wird dann genutzt, um das Suchfenster entweder nach oben oder nach unten weiter einzugrenzen.
NegaC* (Knoten, f):
min = −∞
max = ∞
solange min < max:
med = min + (max − min) / 2
r = alphaBetaMitSpeicher(Knoten, med, med + 1)
wenn r ≤ med:
max = r
sonst:
min = r
gib min zurück
¶ Fazit
Die algorithmische Lösung von Vier Gewinnt stellt eine interessante Herausforderung dar, die sowohl grundlegende als auch fortgeschrittene Techniken der Künstlichen Intelligenz umfasst. Algorithmen wie Minimax und dessen Optimierungen, insbesondere Alpha-Beta Pruning, ermöglichen eine systematische Bewertung von Zügen und verbessern die Effizienz bei der Entscheidungsfindung. Durch die Reduktion des Suchbaums wird die Rechenleistung erheblich gesenkt, wodurch das Spiel in akzeptabler Zeit gelöst werden kann. Allerdings zeigt die Analyse, dass Alpha-Beta Pruning zwar eine weit verbreitete Methode ist, aber nicht die optimale Lösung für Vier Gewinnt darstellt.
In diesem Kontext bieten weiterentwickelte Algorithmen wie PVS (Principal Variation Search), NegaC* und MTD(f) deutlich bessere Ergebnisse und verkürzen die Lösungszeit auf nur wenige Minuten. Diese Methoden berücksichtigen nicht nur die Reduktion des Suchraums, sondern optimieren auch die Art und Weise, wie Züge bewertet und zurückgegeben werden, was zu einer merklichen Beschleunigung der Berechnungen führt.
¶ Offene Punkte
- Visualisierung der Leistungsunterschiede: Grafische Darstellung der Performance von Minimax und Alpha-Beta-Pruning bei steigenden Spielfeldgrößen (n) unter Verwendung realistischer Datensätze, um praxisnahe Unterschiede zu verdeutlichen.
- Non-Feature Heuristik: Ein weiterer interessanter Punkt wäre, wenn im Artikel von Kang et al. [8:1] noch genauer auf die zweite Heuristik eingegangen würde. Der Artikel erklärt zwar, wie die Spielfelder ihre Bewertungen erhalten, jedoch bleibt offen, wie aus diesen Bewertungen letztlich der Wert eines Spielzugs berechnet wird.
¶ Referenzen
Anmerkung: Diese Seite wurde von Marin Dvojkovic verfasst. Änderungen von anderen Personen an diesem Artikel sind nicht mit dem Verfasser abgesprochen.
¶ Abbildungen
Pseudocode 1: Übersetzt aus: Yassin Liese. 2024. Entwicklung eines Frameworks zur systematischen Evaluierung und Optimierung Minimax-basierter Suchstrategien anhand des Spiels Vier-Gewinnt.[10:1]
Pseudocode 2: Übersetzt aus: Yassin Liese. 2024. Entwicklung eines Frameworks zur systematischen Evaluierung und Optimierung Minimax-basierter Suchstrategien anhand des Spiels Vier-Gewinnt.[10:2]
Pseudocode 3: Übersetzt aus: Yassin Liese. 2024. Entwicklung eines Frameworks zur systematischen Evaluierung und Optimierung Minimax-basierter Suchstrategien anhand des Spiels Vier-Gewinnt.[10:3]
Abbildung 1: https://www.zambomba.de/wp-content/uploads/2022/07/Hasbro-Spiel-Brettspiel-Vier-Gewinnt-4-Gewinnt-01.jpg
Abbildung 2: Screenshot aus https://playconnectfour.com/pass-n-play
Abbildung 3: Screenshot aus https://playconnectfour.com/pass-n-play
Abbildung 4: Screenshot aus https://playconnectfour.com/pass-n-play
Abbildung 5: aus David Avellan-Hultman and Emil Gunnberg Querat. 2021. A comparison of two tree-search based algorithms for playing 3-dimensional Connect Four. [4:1]
Abbildung 6: https://www.sciencebuddies.org/51bmjfuB2tMQUMzB1_Pafdt13-k=/750x419/-/https/www.sciencebuddies.org/cdn/Files/20146/8/connect-4-game-tree-diagram.png
Abbildung 7: aus Rijul Nasa, Rishabh Didwania, Shubhranil Maji, and Vipul Kumar. 2018. Alpha-beta pruning in mini-max algorithm–an optimized approach for a connect-4 game.[9:1]
Tabelle 1: Übersetzt aus: Xiyu Kang, Yiqi Wang, and Yanrui Hu. 2019. Research on different heuristics for minimax algorithm insight from connect-4 game. [8:2]
Tabelle 2: Übersetzt aus: Xiyu Kang, Yiqi Wang, and Yanrui Hu. 2019. Research on different heuristics for minimax algorithm insight from connect-4 game. [8:3]
¶ Textquellen
Vier gewinnt. Wikipedia. Retrieved January 16, 2025 from https://de.wikipedia.org/w/index.php?title=Vier_gewinnt&oldid=245279174 ↩︎ ↩︎ ↩︎
Nullsummenspiel. Wikipedia. Retrieved January 18, 2025 from https://de.wikipedia.org/w/index.php?title=Nullsummenspiel&oldid=249408354https://de.wikipedia.org/wiki/Nullsummenspiel ↩︎
Walter Schlee, Einführung in die Spieltheorie: mit Beispielen und Aufgaben, ISBN 3-528-03214-6, S. 95 ↩︎
David Avellan-Hultman and Emil Gunnberg Querat. 2021. A comparison of two tree-search based algorithms for playing 3-dimensional Connect Four. Retrieved January 18, 2025 from https://www.diva-portal.org/smash/record.jsf?pid=diva2:1597267 ↩︎ ↩︎
Abdoul Wahab Touré. 2023. Evaluation of the Use of Minimax Search in Connect-4 —How Does the Minimax Search Algorithm Perform in Connect-4 with Increasing Grid Sizes? AM 14, 06 (2023), 419–427. https://doi.org/10.4236/am.2023.146025 ↩︎ ↩︎ ↩︎
Louis Victor Allis. 1988. A Knowledge-Based Approach of Connect-Four. J. Int. Comput. Games Assoc. 11, 4 (1988), 165. ↩︎
James D. Allen. 1990. Expert Play in Connect-Four. Verfügbar unter https://web.archive.org/web/20131023004851/http://homepages.cwi.nl/∼tromp/c4.html Allis 1988, (1990). ↩︎
Xiyu Kang, Yiqi Wang, and Yanrui Hu. 2019. Research on different heuristics for minimax algorithm insight from connect-4 game. Journal of Intelligent Learning Systems and Applications 11, 02 (2019), 15. ↩︎ ↩︎ ↩︎ ↩︎
Rijul Nasa, Rishabh Didwania, Shubhranil Maji, and Vipul Kumar. 2018. Alpha-beta pruning in mini-max algorithm–an optimized approach for a connect-4 game. Int. Res. J. Eng. Technol 5, (2018), 1637–1641. ↩︎ ↩︎
Yassin Liese. 2024. Entwicklung eines Frameworks zur systematischen Evaluierung und Optimierung Minimax-basierter Suchstrategien anhand des Spiels Vier-Gewinnt. Technische Universität Berlin, Berlin. Retrieved January 16, 2025 from https://doc.neuro.tu-berlin.de/bachelor/2024-BA-YassinLiese.pdf ↩︎ ↩︎ ↩︎ ↩︎