¶ Schach
Schach ist ein strategisches Brettspiel, das von zwei Spielern gespielt wird. Die Spieler bewegen abwechselnd ihre Spielsteine auf dem Spielfeld (dem sogenannten Schachbrett). Das Ziel des Spiels ist es, die gegnerische Königsfigur anzugreifen, nämlich so, dass der angegriffene Spieler keine Möglichkeit mehr hat den Angriff durch das Bewegen einer seiner Figuren abzuwehren. Diese Position nennt sich dann Schachmatt.
¶ Spielregeln
¶ Vorwissen
Schach wird auf einem Schachbrett gespielt. Ein Schachbrett hat 64 Felder bestehend aus 8 Spalten und 8 Reihen. Zu Anfang eines Spiels sind 32 Spielfiguren auf dem Feld. Beide Spieler, der Beginnende Spieler (Weiß), wie auch der Antwortende Spieler (Schwarz), haben jeweils 16 Figuren zur Verfügung: einen König, eine Dame, zwei Türme, zwei Läufer, zwei Springer und acht Bauern.
Diese werden in die Ausgangsaufstellung gebracht, wie auf Abb.1 zu sehen ist. Der weiße Spieler beginnt mit seinem Zug, danach wechseln sich die Spieler fortlaufend ab.
Ein Zug ist nur gültig, wenn der eigene König nach dem Zug nicht im Schach steht (d.h. nicht unter Angriff steht). Bei einem Zug wird entweder
- eine Figur nach den figurspezifischen Regeln bewegt, oder
- eine Rochade gespielt, oder
- ein En-Passant gespielt.
Grundsätzlich darf eine Figur
- auf ein leeres Feld bewegt, oder
- auf ein durch eine gegnerische Figur besetztes Feld bewegt werden (wobei die gegnerische Figur "geschlagen" und vom Spielfeld entfernt wird).
Eine Figur darf jedoch nie, auf ein durch eine eigene Figur besetzes Feld bewegt werden. Auch darf eine Figur nicht über das Spielfeld hinaus gezogen werden, und die Bewegung der Figur an anderer Stelle des Bretts fortgesetzt werden - die Bewegung einer Figur ist stets durch den Spielfeldrand begrenzt.
Das Spiel endet, sobald einer der beiden Spieler keine gültigen Züge mehr hat. In Wettkämpfen existieren darüberhinaus weitere Kritieren, nach denen ein Spiel beendet wird. Mehr dazu unter Spielende.
¶ Zugregeln
¶ König

Der König darf horizontal, vertikal und diagonal auf anliegende Felder (d.h. um genau ein Feld) bewegt werden - somit hat dieser bis zu acht Zugoptionen. Die beiden Könige dürfen niemals nebeneinander stehen (d.h. auch nicht gezogen werden), da sie sich sonst gegenseitig ein Schach liefern würden.
Der König ist ebenfalls Teil der Rochadezugs, der einizge Zug im Schach bei dem zwei Figuren gleichzeitig bewegt werden dürfen. Mehr dazu unter Rochade.
¶ Dame
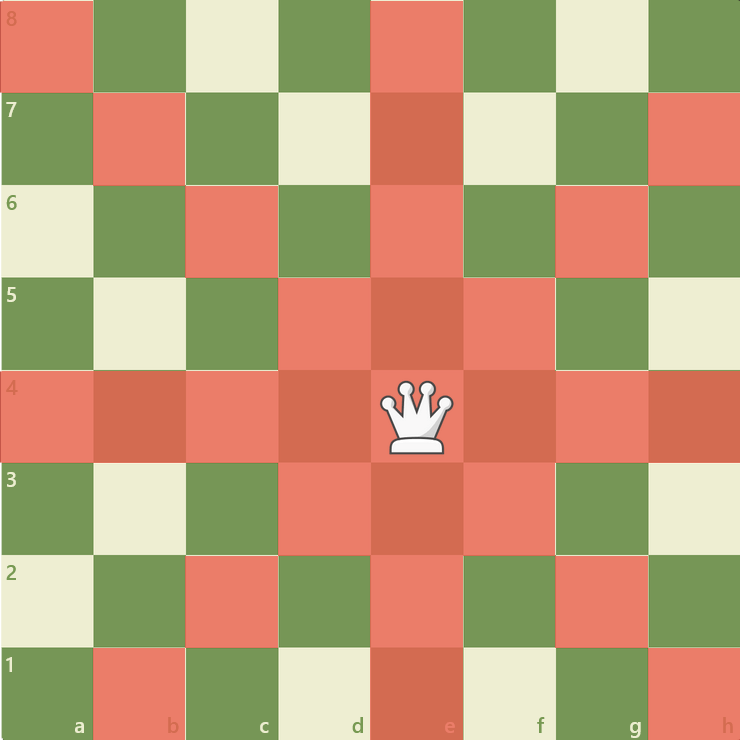
Die Dame darf horizontal, vertikal und diagonal beliebig weit bewegt werden, jedoch ohne dabei Figuren zu überspringen. Die Dame vereint somit die Bewegungsmöglichkeiten eines Turm und Läufers in einer Figur.
¶ Turm

Der Turm darf horiziontal und vertikal beliebig weit bewegt werden, jedoch ohne dabei Figuren zu überspringen.
Der Turm ist ebenfalls Teil der Rochadezugs, der einizge Zug im Schach bei dem zwei Figuren gleichzeitig bewegt werden dürfen. Mehr dazu unter Rochade.
¶ Läufer

Der Läfer darf diagonal beliebig weit bewegt werden, jedoch ohne dabei Figuren zu überspringen.
¶ Springer

Der Springer macht L-förmige Züge. Er darf sich um genau zwei Reihen und einer Spalte bewegen oder umgekehrt, um genau zwei Spalten und einer Reihe.
¶ Bauern
Bauern bewegen sich grundsätzlich immer um genau ein Feld, nämlich in Richtung des Gegners. Ein weißer Bauer hat somit bis zu 3 mögliche Zielfelder: das Feld vor ihm (d.h. das Feld in direkter Richtung zur letzten Reihe, die Achte für Weiß und die Erste für Schwarz), oder die beiden Felder diagonal vor ihm.
- Ein Bauer darf in direkter Richtung um genau ein Feld vorgerückt werden, wenn das Feld vor ihm leer ist.
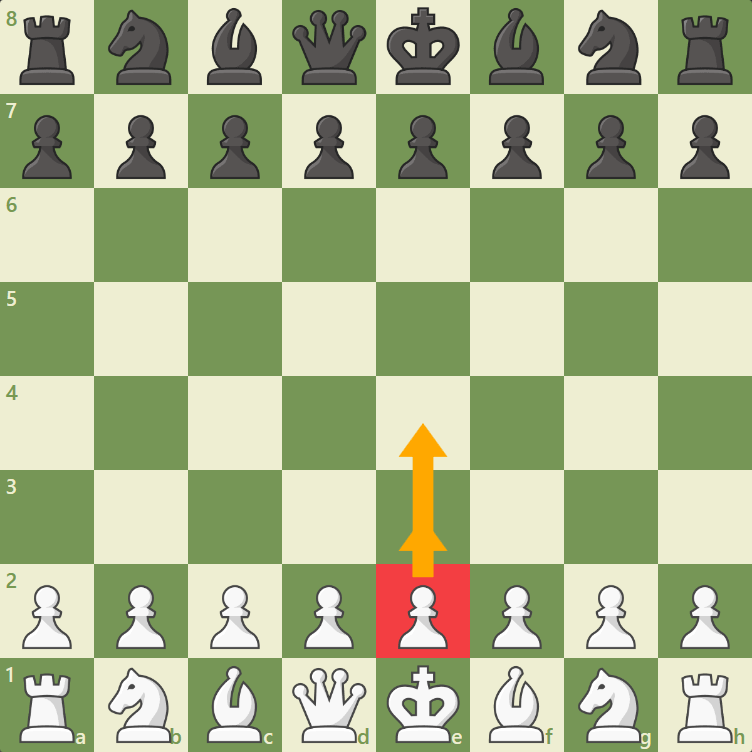
- Steht ein Bauer noch in Anfangsstellung (in der zweiten als Weiß bzw. siebten Reihe als Schwarz) so darf dieser Bauer wahlweise in direkter Richtung um zwei Felder vorgerückt werden, wenn sowohl das Feld vor ihm als auch das Zielfeld leer sind(siehe Abb.7).
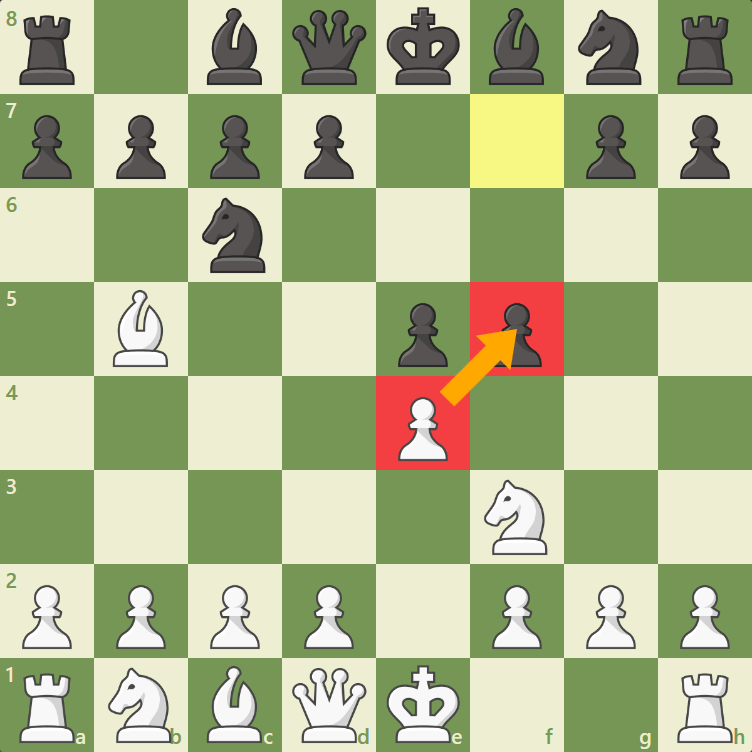
- Steht eine gegnerische Figur auf einem der Diagonalfelder der Bauernfigur, so darf dieser Bauer sich diagonal (vor)bewegen wobei die gegnerische Figur geschlagen wird (siehe Abb.8).
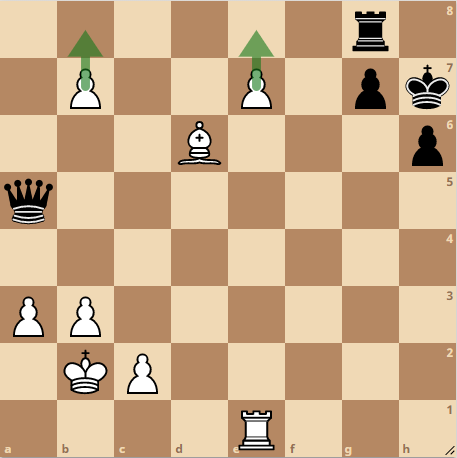
- Bewegt sich der Bauer auf die (von ihm gesehen) letzte Reihe so muss der Bauer bei Ankommen auf dem Zielfeld durch eine Dame, einen Turm, einen Läufer oder einem Springer ersetzt werden. Dieser Vorgang nennt sich Umwandlung und gilt als starker Zug im Schach(siehe Abb.9).
Ein Bauer darf sich niemals diagonal (vor)bewegen, es sei denn auf dem Diagonalfeld steht eine gegnerische Figur. Einzige Ausnahme ist der En-Passant-Zug, bei welchem ein Bauer sich diagonal auf ein leeres Feld bewegen darf. Mehr dazu unter En-Passant.
¶ Rochade
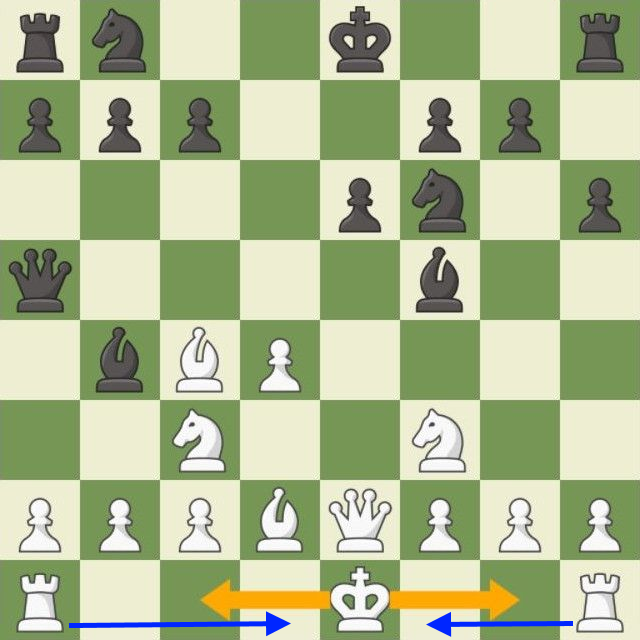
Die Rochade ist der einzige Doppelzug im Schach - bei diesem werden der König und ein Turm gleichzeitig bewegt. Jeder Spieler darf die Rochade höchstens einmal spielen und nur dann, wenn
- der Spieler noch nie den König und den entsprechenden Turm bewegt hat
- keine Figuren zwischen König und Turm stehen
- der König weder im Schach steht, sich während der Rochade durch Schach bewegen würde oder nach der Rochade im Schach steht
Bewegt ein Spieler einen Turm so verwirkt der Spieler sein Recht auf Rochade zu dieser Seite. Bewegt ein Spieler beide Türme oder den König so verwirkt der Spieler sein Recht auf Rochade gänzlich.
Bei der Rochade bewegt sich der König zwei Felder in Richtung des entsprechenden Turms und der Turm bewegt sich auf das Feld was soeben vom König übersprungen wurde (siehe Abb.10).
¶ En-Passant

Hat ein gegnerischer Bauer einen Doppelschritt gemacht, so darf, wenn der eigene Bauer das vom gegnerischen Bauern übergangene Feld diagonal angreift, sich der Bauer diagonal auf das übergangene Feld vorbewegen und schlägt dabei den gegnerischen Bauern, als hätte dieser auf dem Zielfeld gestanden. Dieser sogenante En-Passant Zug muss direkt auf den Doppelschritt des Gegeners folgen, anderfalls verfällt das En-Passant Recht.
¶ Spielende
Hat einer der beiden Spieler keine gültigen Züge mehr so endet das Spiel. War der Spieler, der keinen Zug mehr machen konnte, im Schach, so verliert er das Spiel. War der Spieler allerdings nicht im Schach, so endet das Spiel in einem Unentschieden (ugs. "Remi durch Patt").
Im Wettkampfs-Schach wird überlicherweise mit Zeitkontrolle gespielt, d.h. beide Spieler haben nur eine gewisse Menge an verfügbare Zeit.
Weitere Gründe für das Enden einer Schachpartie sind:
- Sieg durch Ablaufen der verfügbaren Zeit des Gegners
- Sieg durch Aufgabe des Gegners
- Unentschieden durch Einigung auf Remi
- Unentschieden durch die Fünfzig-Zug-Regel
- Falls beide Spieler in ihren letzten 50 Zügen weder einen Bauern bewegt noch eine andere Figur geschlagen haben, so kann ein Unentschieden beansprucht werden.
- Unentschieden durch Wiederholung
- Falls während eines Schachspiels dreimal die gleiche Stellung auftritt, so kann ein Spieler ein Unentschieden beanspruchen. Gleiche Stellung bedeutet, dass die Figuren auf den gleichen Feldern stehen, der gleiche Spieler am Zug ist und die Rochade- und En-Passant Rechte gleich sind.
- Technisches Unentschieden
- Es gibt Stellungen im Schach aus denen keiner der beiden Spieler einen Sieg erzwingen kann (z.B. König vs. König, König vs König und Läufer)
¶ Komplexität
Schach ist ein Zwei-Personen-Nullsummenspiel mit perfekter Information ohne Zufallskomponente und ist daher determiniert[1]. Das bedeutet, dass (zumindest in der Theorie)
- eine Gewinnstrategie für Weiß existiert, oder
- eine Gewinnstrategie für Schwarz existiert, oder
- das Spiel in einem Unentschieden endet.
Schach gilt in der Praxis jedoch weiterhin als ungelöst. Die Suchbaumkomplexität von Schach wurde 1950 von Claude Shannon mit ungefähr 10120 (auch bekannt als Shannon Number) und die Zustandskomplexität mit etwa 1043 abgeschätzt[2]. Aktuellere Schätzungen, bewegen sich in ähnlichen Bereichen (z.B. durch Viktor Allis im Jahr 1997 mit 10123 Zugvarationen und 1050 mögliche Schachstellungen)[3].
¶ Lösungsansätze
¶ Geschichte
Der Mathematiker und Informationstheoretiker, Claude Shannon, begab sich bereits im Jahre 1950 in die Tiefen der Schachforschung. Seine wegweisende Publikation "Programming a Computer for Playing Chess" [2:1] markiert den einleitenden Schritt in die Entwicklung von Schachprogrammen.
Er berechnete, dass bei einer Berechnungsgeschwindigkeit von einer Variation pro Mikrosekunde (sehr optimistisch für damalige Zeiten) bereits 1090 Jahre für die Berechnung des ersten Zuges notwendig wären .
Shannon kam zu dem Schluss, dass es ungeeignet sei, Schach mithilfe von Brute-Force zu lösen. Stattdessen sollten Schachprogramme lieber approximative Methoden verwenden, mit dem Ziel, dennoch besser als der Mensch zu spielen. Trotz des Verzichts auf die tatsächliche Brute-Force-Lösung und der Anwendung von approximativen Methoden sind heutige Schachprogramme in der Lage, selbst Großmeister konsistent zu schlagen.
In seiner Arbeit führte er das Konzept von approximativ arbeitenden Schachprogrammen ein, die des Typs A und die des Typs B. Typ A verfolgt einen Brute-Force-Ansatz, indem er alle Suchbaumpfade bis zu einer gewissen Tiefe erfasst, während Typ B selektiv arbeitet und ausschließlich vermeintlich "wichtige" Suchbaumpfade untersucht, ähnlich zu menschlichem Schachspiel. Obwohl Shannon den Typ B bevorzugte, zeigen heutige Schachprogramme tendenziell mehr Ähnlichkeiten mit Typ A, was vermutlich auf die gesteigerte Rechengeschwindigkeit zurückzuführen ist. Nichtsdestotrotz integrieren moderne Schachprogramme Aspekte sowohl von Typ A als auch von Typ B.
¶ Suchbaumalgorithmen
Die Anwendung von Suchbaumalgorithmen im Schach ist von essenzieller Bedeutung, um optimale Spielzüge zu ermitteln. Heutzutage benutzen viele der besten Schachprogramme wie z.B. Stockfish, Berserk, Caissa, RubiChess und Obsidian.1 sogenannte Depth-First-Search (DFS) Algorithmen (meist eine Form der Alpha-Beta-Suche).
Trotz der Dominanz von DFS-Algorithmen haben sich im Laufe der Jahre aber auch vereinzelt Programme entwickelt, die auf Best-First-Search-Algorithmen wie Monte-Carlo-Tree-Search (MCTS) setzen. Ein herausragendes Beispiel ist AlphaZero[4], welches 2018 mithilfe von MCTS mit dem damalig stärksten DFS-basierendem Schachprogramm Stockfish konkurrieren konnte 2,3. In Anbetracht der Tatsache, dass der Sourcecode von AlphaZero nicht öffentlich einsehbar ist, entwicklete sich die Open-Source Engine Leela Chess Zero, welches ähnlich zu AlphaZero, MCTS nutzt. Leela Chess Zero belegt seit 2020 regelmäßig den zweiten Platz (hinter Stockfish) im Top Engine Chess Championship 4.
¶ Schachrechner
In diesem Wiki liegt der Fokus explizit auf Alpha-Beta-basierten Schachrechnern. Andere Ansätze und Algorithmen, die nicht auf Alpha-Beta basieren, werden in diesem Kontext nicht weiter beleuchtet.
¶ Funktionsweise
Ein Großteil der heutigen starken Schachrechner basieren auf Alpha-Beta-Suche und bestehen meist aus drei Hauptkomponenten: dem Eröffnungsbuch, der Suche (inkl. Evalutation) und einer Endspieldatenbank.
-
Eröffnungsbuch
Bevor ein Schachrechner mit der zeitintensiven Suche beginnt, greift er auf das Eröffnungsbuch zurück, in welchem vorprogrammierte und etablierte Eröffnungszüge enthalten sind. Das Eröffnungsbuch bildet somit die Grundlage für einen schnellen und kenntnisreichen Start in die Partie. -
Suche & Evaluation
Sobald die Schachpartie das Anfangsstadium verlässt, setzen Schachrechner eine Suche ein (in der Regel eine Alpha-Beta-Suche), um den besten Zug zu ermitteln. Im Verlauf dieser Suche wird eine Evaluationsfunktion verwendet, um abzuschätzen, wie gut oder schlecht eine Position ist. Diese beiden Aspekte – die Suche und die Evaluation – bilden die zentralen Punkte, die durch zahlreiche kleine kumulative Verbesserungen erhebliche Steigerungen in der Spielstärke von Schachrechner bewirken können. -
Endspieldatenbank
Die Endspieldatenbank bildet den dritten Baustein und enthält vorberechnete Endspielstellungen.Die Endspieldatenbank ermöglicht es dem Schachrechner, in den finalen Phasen des Spiels präzise Evaluationen durchzuführen, da er auf bereits vollständig analysierte Endspielpositionen (Weiß/Schwarz gewinnt/Unentschieden) zurückgreifen kann, anstatt auf eine heuristik-basierte Evaluationsfunktion.
¶ Alpha-Beta-Suche
Die Alpha-Beta-Suche ist eine optimierte Version des Minimax-Algorithmus. Die Alpha-Beta-Suche kann durch weitere Optimierungen verfeinert werden, wodurch die Suche allerdings imperfekt wird. Die Herausforderung besteht darin, die Suche effizient zu gestalten, ohne dabei durch die Imperfektion der Suche übermäßig viele ungenaue Ergebnisse zu generieren. Die meisten Optimierungen lassen sich meist einer oder mehreren der folgenden Kategorien zuordnen:
- Effiziente Ergebniswiederverwendung:
Wiederverwendung von Ergebnissen besuchter Teilbäume.
- Optimierte Zugreihenfolge:
Verbesserung der Untersuchungsreihenfolge von Zügen. - Anpassung des Suchfensters:
Anpassung der Fensterbreite unter Verwendung von Heuristiken, um die Anzahl and Cut-Offs zu maximieren. - Suchpfadspezifisches Pruning
Dynamische Anpassung der Suchpfadtiefen bzw. Pruning durch Integration bestimmter Heuristiken.
¶ Optimierungen von Alpha-Beta-Suche
-
-
Iterative Tiefensuche
Die iterative Tiefensuche (engl. Iterative Deepening) bildet den Grundbaustein (quasi) aller weiteren Optimierungen. Die Idee dabei besteht darin, anstelle einer direkten Suche bis zur Tiefe die Suche iterativ durchzuführen, beginnend mit der Tiefe und anschließend gestaffelt bis zur Tiefe . Dieser Ansatz hat zwei Hauptgründe: Erstens spielen Schachrechner oft unter Zeitkontrolle, und es ist vor Beginn einer -tiefen Suche unklar, wie lange diese dauern wird. Daher starten Suchen bei Tiefe 1 und steigern sich im Verlauf, sodass selbst bei Auslaufen der Zeit ein Ergebnis vorliegt [5]. Zweitens hat sich gezeigt, dass die iterative Tiefensuche tatsächlich schneller als eine normale Suche ist.[6] Dies liegt daran, dass Ergebnisse aus vorherigen Suchen für tiefere Suchen wiederverwendet werden können (siehe Move Ordering) und iterative Tiefensuche Informationen für weitere dynamische Optimierungen (wie 2,3,4) erzeugt. -
Transposition Tables
Wie das Wort Transposition andeutet, gibt es im Schach Positionen, die durch verschiedene Zugreihenfolgen entstehen können. Zwei solcher Positionen werden als Transpositionen bezeichnet. Es wäre unpraktisch, jedes Mal, wenn man auf eine solche Position trifft, den gesamten Teilbaum erneut auswerten zu müssen. Hier kommen Transposition Tables zum Einsatz. In diesen Tabellen werden Informationen zu bereits analysierten Positionen gespeichert. Wenn man auf eine bereits bekannte Position trifft, kann man die bereits berechnete Evaluation aus der Tabelle nutzen [7].
Um Informationen in der Tabelle zu speichern und zu finden, muss jedoch ein Weg gefunden werden, um Positionen auf einen Index in der Tabelle abzubilden. Hierfür wird sogenanntes Zobrist-Hashing[8] verwendet. Die Grundidee des Zobrist-Hashings besteht darin, für jedes Figur-Feld-Paar eine zufällige (typischerweise) 64-Bit Zahl zu generieren. Ebenso erhalten weitere spielzustandsverändernde Flags, wie Rochaderechte, eine zufällige 64-Bit Zahl. Beim Zobrist-Hashing wird nun die eXklusive OR-Operation (XOR) auf die zufälligen Zahlen der relevanten Felder und Flags angewendet. Der Vorteil dieses Hashing-Verfahrens liegt in der Umkehrbarkeit des XOR, wodurch Zobrist-Hashes inkrementell, das heißt effizient, aktualisiert werden können. -
Quiescence Search
Leider ist die Evaluationsfunktion im Schach nur eine Approximation für die Güte einer Position. Bei der Suche bis zu einer bestimmten Tiefe besteht nun die Gefahr, dass wichtige Bewertungsaspekte für die Evaluation übersehen werden, da sie über dem "Horizont", d.h. erst in einer tieferen Suche sichtbar werden. Dieses Phänomen nennt man Horizon Effect[9]. Ein Beispiel ist hierfür, wenn in einem Blattknoten - also am Horizont - eine Dame einen Bauern geschlagen hat. Die Evaluation bewertet dies möglicherweise als positiv, da eine Figur geschlagen wurde. Hätte man jedoch einen Halbzug tiefer gesucht, so hätte man gesehen, dass die Dame eventuell züruckgeschlagen wird, was nachteilig ist. Quiescence search[10], ist der Versuch, den Horizon Effect zu mildern. Die Idee besteht darin, die normale Suche zu erweitern, nämlich so weit, bis man in einer ruhigen (engl. quiet) Position gelangt ist. In ruhigen Positionen ist die (statische) Evaluation präziser. Typische unruhige Positionen sind Positionen, in denen eine Figur geschlagen werden kann, eine Umwandlung möglich ist oder der König im Schach steht.
-
-
Optimierung durch Selektivität
- Move Ordering
Alpha-Beta-Suche ist besonders effizient, wenn die Zugsortierung gut ist d.h. wenn der theoretisch beste Zug als Erstes und der theoretisch schlechteste Zug als Letztes untersucht wird. In diesem Fall treten besonders frühe Cut-offs im Suchbaum auf. Bei perfekter Zugsortierung kann bei der gleichen Anzahl an untersuchten Knoten etwa doppelt so tief (im Vergleich zum Minimax-Algorithmus) gesucht werden [11]. Es gibt viele Wege die Züge zu sortieren, sowohl dynamisch als statisch. Einer der wichtigsten (dynamischen) Heuristiken ist es den besten Zug aus der letzten Iteration (für die gegebene Position) als erstes zu untersuchen. Diese Information ist in der Transposition Table gespeichert. Eine weitere (statische) Heuristik ist es besonders vielversprechende Schläge (engl. Captures) zu priorisieren, d.h. wenn eine weniger wertvolle Figur, eine sehr wertvolle Figur schlägt[11:1]. Über die Jahre haben sich auch vermehrt Versuche ergeben, die Zugsortierung mit KI Methoden zu lernen [12][13]. - Extenstions/Reductions/Pruning
Extensions und Reductions sind Heuristiken, um besonders vielversprechende Suchbaumpfade tiefer zu durchsuchen und weniger vielversprechende Pfade eher "flach" zu behandeln. Pruning hingegen ist eine noch aggressivere Methode, bei der bestimmte Pfade gänzlich unberücksichtigt bleiben, um die Suchraumgröße stark zu reduzieren. Explizite Methoden werden im Artikel Selektivität vorgestellt.
- Move Ordering
-
Optimierungen durch Anpassung von Alpha und Beta
-
Principal-Variation-Search
Principal-Variation-Search ist eine performantere Variante der Alpha-Beta-Suche, wenn eine gute Zugsortierung vorliegt. Bei PVS wird der erste Zug mit einem vollem Fenster untersucht, d.h. nach der Untersuchung des ersten Zuges ist . Für alle weitere Züge bestätigt man mithilfe einer Null-Fenster-Suche , dass diese tatsächlich schlechter als der erste, vermeintlich beste, Zug sind. Gibt die Null-Fenster-Suche jedoch einen Wert über züruck, d.h. es existiert ein Zug der besser als der erste Zug ist, so muss die Suche mit einem vollem Fenster wiederholt werden. Aus diesem Grund ist PVS nur besser, wenn der theoretisch beste Zug fast immer als Erstes untersucht wird[14]. -
Aspiration Windows
Typischerweise wird eine Alpha-Beta-Suche mit dem Initialfenster und gestartet. Aspiration Windows ist die Idee, die Evaluation aus der letzten Iteration der iterativen Tiefensuche zu nutzen, um die Breite des Initialfensters der Iteration sinnvoll zu verkleinern und so frühere Cut-Offs zu erreichen. Evaluationen sind im Schach meist in Bauerneinheiten kalkuliert. Aspiration Windows von etwa plus/minus einer Bauerneinheit um führen in der Praxis zu guten Ergebnissen [15].
-
¶ Evaluation
Die Bewertung einer Schachposition erfolgt durch eine Evaluationsfunktion, die den relativen Wert dieser Position bestimmt. Optimalerweise nimmt diese Evaluationsfunktion nur drei Werte an: 1 (Sieg aus dieser Position), 0 (Unentschieden aus dieser Position) und -1 (Niederlage aus dieser Position). In diesem Fall könnten wir unmittelbar feststellen, welcher Spieler gewonnen hat, und eine Suche der Tiefe 1 wäre ausreichend, um den optimalen Zug zu identifizieren.
In der Praxis existiert jedoch keine Funktion, die den exakten Wert einer Position bestimmt3. Aus diesem Grund wird die Evaluationsfunktion benutzt um den relativen Wert einer Position zu approximieren. Das Ziel besteht darin, diese Approximation so präzise wie möglich zu gestalten. Das bedeutet, wenn Zug B die theoretische Antwort auf Zug A ist, sollten die Evaluationen der Positionen nach den Zügen A und B möglichst den gleichen Wert aufweisen. Insbesondere bedeutet dies, dass nicht der exakte Wert der Evaluationsfuntkion wichtig ist, sondern die relativen Wahrscheinlichkeiten des Gewinnens[16].
Nach welchen Aspekten eine Schachposition bewertet wird ist dem Entwickler ueberlassen. Wie Shannon 1950 erkannte, erscheint es jedoch sinnvoll, sich an Bewertungskriterien des menschlichen Spieles zu orientieren.
"Any good chess player must, in fact, be able to perform such a position evaluation. Evaluations are based on the general structure of the position, the number and kind of Black and White pieces, pawn formation, mobility, etc. These evaluations are not perfect, but the stronger the player the better his evaluations. Most of the maxims and principles of correct play are really assertions about evaluating positions, for example:
[...]"[2:2]
Im Folgenden sind einige gaengige Aspekte gelistet, die im menschlichen Spiel beruecksigt werden und in die Evaluation eines Schachrechners mit einfließen koennen.
- Material
Es ist grundsätzlich gut, mehr und bessere Figuren als sein Gegner auf dem Spielfeld zu haben. Verschiedene Schachfiguren haben dabei verschiedene Wertigkeiten. Der Bauer ist aufgrund seiner eingeschränkten Bewegungsmoeglichkeiten die schwaechtse Figur auf dem Feld. Die Dame hingegen ist aufgrund ihrer großen Bewegungsfreiheit besonders stark. Eine mögliche Gewichtung der Figuren ist (1 = Bauer), (3 = Springer = Laeufer), (5 = Turm), (9 = Dame)[2:3]. - Position der Figuren
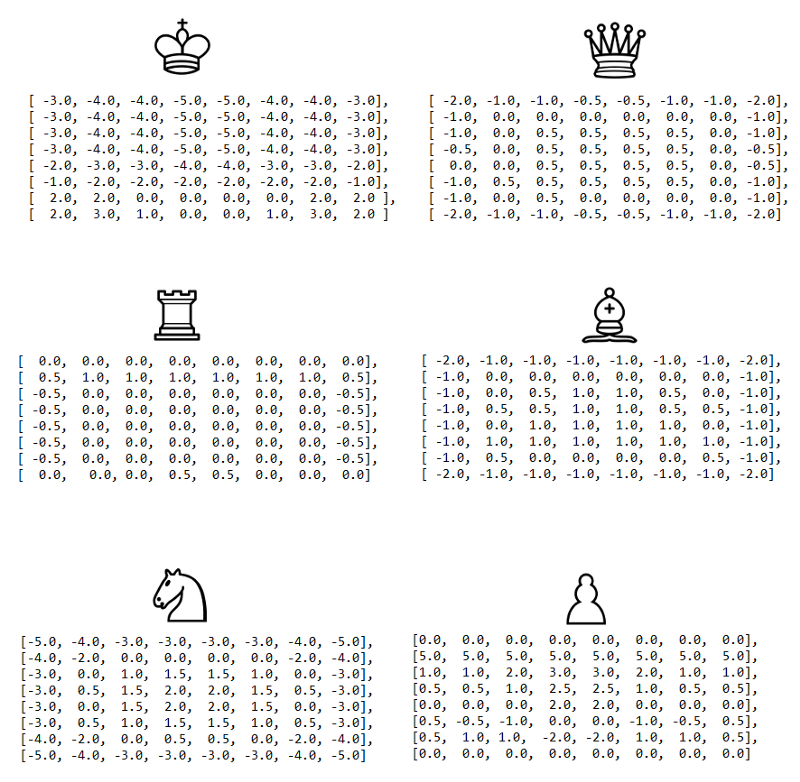
Die verschiedenen Figuren des Schachs sind abhängig ihres Feldes besonders stark oder schwach. Beispielsweise ist ein Springer am Rand der Schachbretts, eher schwach, da er nur 3-4 aus den moeglichen 8 Feldern die er kontrollieren koennte, kontrolliert. Bauern sollten im Laufe des Spiels grundsätzlich in die gegnerische Hälfte vorbewegt werden, mit Chance auf Umwandlung. In der Praxis benutzt man hierfür oft, sogenannte Piece-Square-Tables6: für jede Figur existiert eine Tabelle in der für jedes Feld ein Bonus oder Malus enthalten ist (siehe Abb.12). Die Tabellen können entweder händisch erstellt oder mit KI-Methoden wie TD-learning[17][18] und Regression gelernt und verbessert werden. - Königssicherheit
Im Laufe des Spiels sollte kontinuerlich auf die Sicherheit der Königsfigur geachtet werden. Die Erfahrung aus menschlichem Schachspiel zeigt, dass insbesondere die Rochadefelder recht sichere Felder fuer den König sind7. Dies lässt sich z.B. mit Piece-Square-Tables verbinden, sodass es für die Rochadefelder besonders grosse Boni gibt (siehe Abb.12). Insgesamt ist die Königssicherheit jdeoch ein sehr schwer zu bewertender Aspekt. Gerade im Endpsiel, ist es wichtig, dass der König auch aktiv wird und die wenig verbleibenden Figuren unterstüzt7. Boni fuer Rochadefeldern und Mali für gegnerische Felder können dann schnell zum Nachteil werden und die Evaluationsfunktion unpräzise machen. - Bauernstruktur
Es is grundsätzlich schlecht isolierte Bauern - Bauern die durch keine anderen Bauern geschützt sind -, sowie Doppelbauern - Bauern die durch das Schlagen einer gegnerischen Figur auf die gleiche Spalte gelangt sind - zu besitzen. Freibauern - Bauern die auf dem Weg zur Umwandlung durch keinen gegnerischen Bauern mehr geschlagen werden könnten - sind besonders attraktiv7. Es kann daher gut sein solche Fälle in der Evaluationsfunktion zu berücksichtigen. - Kontrolle der Zentralfelder
Die Kontrolle der Zentralfelder geht Hand in Hand mit der Position von Figuren. Es ist grundsätzlich gut, die Figuren in das Zentrum des Spielfeldes zu bewegen, da von hier aus maximal viele Felder kontrolliert werden 7. Es ist ebenfalls gut Zentralfelder durch angrenzden Felder zu kontrollieren. Auch dieser Aspekt laesst sich mit Piece-Sqaure-Tables kompinieren, sodass Zentralfelder einen besonders großen Boni enthalten (siehe Abb.12). - Fesselung
Gefesselte Figuren sind Figuren, die nicht bewegt werden koennen, da sie sonst einen gegnerischen Angriff auf den König (oder einer sonst wertvolleren Figur) freilegen wuerden. Solche Figuren haben daher grundsaetzlich einen niedrigeren Wert und was negativ in die Evaluation mit einfließen kann. - Mobilitaet
Es ist meist von Vorteil, wenn die eigenen Figuren aktiver und weniger in ihrer Bewegung eingeschränkt sind, als die des Gegners 7. Ein einfach zu berechnendes Maß der Mobilitaet koente daher die Differenz an möglichen Zuegen sein. - Spielphasen
Abhängig von der Spielpahse sind einige Figuren und Aspekte besonders wichtig oder unwichtig. Ein Beispiel hierfür ist die bereits angesprochene Königsfigur. Gerade am Anfang sollte der König eher sicher auf dem Spielbrett stehen, zum Ende jedoch aktiv werden um eigene Figuren zu unterstuetzen. Veränderte Rollenbedeutungen sollten daher möglicherweise in der Evaluation berücksichtigt werden.
Die oben angeführten Aspekte, sind nur einige der vielen Aspekte nach denen eine Position bewertet werden kann. Die einzelnen Kriterien werden miteinander verbunden. Eine simple Evaluationfunktion könnte sich dabei als Linearkombination der einzelenen Aspekte ergeben [2:4][19][20].
Vermehrt werden auch Spielphasen berücksichtigt, da verschiedene Aspekte in verschiedenen Phasen - der Natur des Spieles wegen - unterschiedliche Gewichtungen haben. Dies kann beispielsweise durch sogenanntes Tapered Evaluation[20:1] erreicht werden. Dabei findet man für die verschiedenen Spielphasen, z.B. Anfangs/Mittel-, und Endstadien, eigene Evaluationsfunktionen. Diese werden dann wieder durch Linearkombination verknüpft, beispielsweise so, dass ein größerer Anteil der Endstadienevaluation einfließt, wenn sich das Spiel im Endstadium befindet, und umgekehrt. Eine konkrete Umsetzung dieser Idee könnte wie folgt aussehen:
wobei ein Maß dafuer ist, wie sehr sich das Spiel im Anfangsstadium befindet.
Für Stockfish, eines der leistungsstärksten Schachprogramme weltweit9, gibt es ein Wiki für dessen Evaluation10. Dort können die verschiedenen Aspekte und die Tapered Evaluation nachvollzogen werden.
Im Jahr 2015 flossen in Stockfish ganze 9 Aspekte in die Evaluation mit ein: Material, Piece-Square Tables, Bauern Struktur, Figur-spezifische Evaluation, Mobilität, Königssicherheit, Gefahr, Raum und "Unentschiedenheit".[16:1]. Bereits ein Jahr zuvor, 2014, hatte Stockfish (zu der Zeit stärkster Schachrechner der Welt) den Grossmesiter Hikaru Nakamura mit 3 zu 1 besiegt8.
¶ Optimierungen von Evaluation
Eine Evaluationsfunktion, die auf einer linearen Kombination basiert, kann auf unterschiedliche Weisen optimiert werden. Dabei spielt die Ermittlung passender Gewichtungen eine Rolle, ebenso wie die Auswahl geeigneter Aspekte. Für linear kombinierte Evaluationsfunktionen ist wichtig, Aspekte zu wählen, die möglichst linear unabhängig sind. In der Praxis sind viele Bewertungsaspekte jedoch nicht perfekt linear unabhängig, wie zum Beispiel Königssicherheit und Bauernstruktur. Es ist oft wünschenswert, dass der König sich hinter Bauern "verstecken" kann 7, was jedoch im Widerspruch zu einer isolierten Betrachtung der Bauernstruktur stehen kann. Hier zeigt sich bereits einer der deutlichen Nachteile einer simplen Modellierung von Evaluationsfunktionen durch lineare Kombinationen.
-
Ungelernte Optimierung
Optimierungen können manuell vorgenommen werden. In diesem Prozess werden neue Bewertungsaspekte (wie Material, Position etc.) geschaffen und die Gewichtungen der einzelnen Aspekte angepasst. Anschließend erfolgt die Testphase, in der die neue Version gegen alte Versionen bzw. andere Schachrechner spielt. Dabei werden die Änderungen beibehlaten, die zu einer Verbesserung geführt haben. Ungelernte Optimierung hat den Nachteil, dass es sowohl langsam ist wie auch durch die Kreativität des Entwicklers beschränkt ist. Mitunter aus diesem Grund haben sich über die Jahre viele Versuche ergeben, Evaluationsfunktionen mit automatischen Methoden zu lernen wie z.B. im Schachrechner Giraffe[16:2]. -
Gelernte Optimierung
Gelernte Optimierung setzt auf automatisierte Methoden, um die Evaluationsfunktion eines Schachprogramms zu verbessern. Über die Jahre haben sind viele Methoden genutzt worden, darunter:- Evolutunäre/Genetische Algorithmen[19:1][21][22]
- Logistische Regression11
- Neuronale Netzwerke[23]
- TD-Learning[17:1][18:1][23:1][24]
¶ Genetische Algorthimen
Verbesserungen der Evaluation durch Evolutionäre Algorithmen konnten bspw. 2010 gezeigt werden, aus dessen Arbeit[21:1] folgenden Grafiken (siehe Abb.13 und Abb.14) entnommen sind. Diese zeigen die deutliche Leistungssteigerung, sodass bereits nach der siebten Evolution, aus 50 Spielen, 11 Spiele mehr gegen den 1700 ELO bemessenenen Schachrechner Rybka , und 19 Spiele mehr gegen den 1900 ELO bemessenenne Schachrechner Rybka gewonnen wurden.
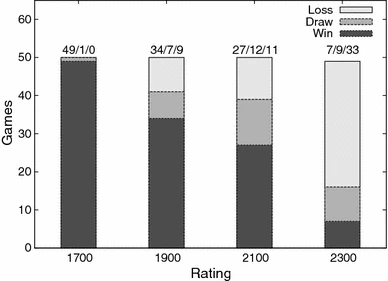
Abb.14 - Siege/Unentscheiden/Niederlage nach 7 Evolutionen 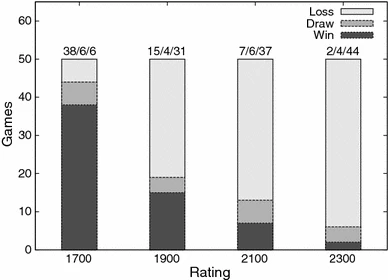
Abb.13 - Siege/Unentscheiden/Niederlage vor Evolution ¶ Regression
Mithilfe einfacher logistischer Regression, konnte der Schachrechner Texel - nach welchem auch die Parametertuning Methode Texel tuning benannt ist - neben anderen Verbesserungen des Programmes, seine Evaluation so sehr verbessern, dass dieser bereits in Version 1.04 eine Spielstärke von 2995 Elo erreichte[16:3]. Zum Vergleich: Magnus Carlsen der stärkste Schachspieler der Welt hatte Stand Januar 2024 eine ELO von 283012.
¶ Neuronale Netzwerke
Erste Versuche der Anwendung von Neuronalen Netzwerken wie z.B. 1994 im experimental Schachrechner, NeuroChess[23:2], zeigten vorerst keine großen Erfolge. Dieser benutze NN und TD-Learning und gewann gerade mal 13% der Spiele gegen den gleichen Schachrechner mit linearer Evaluationsfunktion. Hauptgrund für die schlechten Ergebnisse wurden damals die deutlich längere Berechnungszeit für die Evalution ausgemalt, die der erhöhten Suchtiefe der schnelleren Berechnung der linearen Evaluation unterlegen war.
Erst im Jahr 2018 entwicklete Yu Nasu[25], ursprünglich für das Spiel Shogi, das effizient zu berechnende NNUE (Abk. für: efficiently updatable neural network). Die Grundidee des Netzwerkes ist es, als Input sogennante King-Piece-Encodings zu benuzten - mit der Idee - die Beziehung zwischen dem König und den restlichen Figuren auf dem Feld abzubilden.
Heute kommt NNUE, in angepasster und verbesserter Form, in den meisten der starken Schachprogrammen vor wie z.B. Stockfish, Berserk, und Caissa (Platz 1,4,7 der Computer Chess Rating List).
Für weitere Informationen ist hier eine sehr detaillierte Beschreibung des NNUE Netzwerks von Stockfish.
¶ Erweiterungen
¶ Eröffnungsbuch
Das Eröffnungsbuch enthält eine umfangreiche Sammlung von vorprogrammierten etablierten Schacheröffnungen. Die Nutzung eines Eröffnungsbuches ermöglicht es Schachrechnern, strategisch fundierte Eröffnungszüge zu wählen, ohne dabei eine Suche durchzuführen. Dies hat zwei große Vorteile:
- Einerseits ermöglicht es eine beschleunigte Spielöffnung, da der Computer bereits vorprogrammierte Kenntnisse über die besten Eröffnungszüge besitzt. Dadurch spart er wertvolle Rechenzeit, die später in komplexeren Phasen des Spiels eingesetzt werden kann.
- Obwohl Schachrechner in der Lage sind, komplexe Berechnungen durchzuführen und Millionen von Positionen zu analysieren, fehlt es ihnen an einem tieferen Verständnis für den strategischen Kontext. Gerade in den anfänglichen Spielstadien hilft es daher, eine solide Positionierung aufzubauen und eine strategische Grundlage zu schaffen.
Typischerweise wird ein zufälliger Zug aus einer Menge aus Zugkandidaten gewählt, was insbesondere den Vorteil einer hoeheren Spielvaraition hat (da Schachprogramme ohne Eroeffnungsbuch mehr oder weniger determinisch arbeiten). Eröffnungsbücher können jedoch auch während des Spiels verbessert werden, sodass erfolgreichere Eröffnungszüge in Folgespielen präferiert werden[26][27].
¶ Endspieldatenbank
Die Idee von Endspieldatenbanken ist es, für eine bestimmte (sehr begrenzte) Anzahl an Figuren, für alle Figuren-Feld-Kombinationen die theoretische Lösung zu kalkulieren. Wird in der Evaluation festgestellt, dass nur noch eine sehr begrenzte Anzahl von Figuren auf dem Spielfeld ist, so wird die Evaluation nicht mehr durch Heuristiken berechnet, sondern die Lösung aus der Datenbank genutzt. Bereits bei 3-Figuren ergeben sich 368079 viele Stellungen13. Stand 2018 sind Endspieldatenbanken bis zur einer Figurenanzahl von 7 berechnet worden[28]. Solch große Datenbanken sind jedoch nur in der Theorie nützlich, da bei dieser Größe bereits 140 Terabyte zur Speicherung nötig sind.
¶ Fußnoten
1 Die angegebenen Schachprogramme sind alle unter den Top-10 Schachprogramme Stand Januar 2024. Weitere Beispiele für Alpha-Beta basierte Schachprogramme sind ebenfalls auf der Liste zu finden.
2 Durch die enorme Anzahl an notwendigem Training und der Tatsache, das AlphaZero nicht für die Öffentlichkeit einsehbar ist, behält die Dominanz von AlphaZero gegenüber Stockfish einen pfaden Beigeschmack.
3 Mehr Informationen zum Duell Stockfish vs AlphaZero hier.
4 Erst- und Zweitplatzierung seit 2010 hier.
5 Sonst wäre Schach bereits geloest
6 Viele der hier gelisteten Schachrechner benutzen (oder haben in früheren Versionen) Piece-Square-Tables benutzt, wie z.B. Stockfish, RofChade, Pesto, Texel etc.
7 Viele der Heuristiken sind im Buch Chess the easy way aus dem Jahr 1942 von Rueben Fine, einem ehemaligen Schachgroßmeister, zusammengefasst worden und gelten auch noch noch als gute Praxis.
8 Siehe hier
10 Stockfish benutzt mittlerweile NNUE. Die Evaluierung bezieht sich hier auf die non-NNUE Evaluierung 2020.
11 Der Schachrechner Texel ist ein bekannter Schachrechner der logistische Regression genutzt hat hat um seine Evaluation zu verbessern.
12 Siehe hier
13 Siehe hier für mehr Informationen zu Endspielstellungen
¶ Referenzen
Zermelo, Ernst. "Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels." Proceedings of the fifth international congress of mathematicians. Vol. 2. Cambridge: Cambridge University Press, 1913. S. 501-504. pdf ↩︎
Shannon, Claude E. "Programming a computer for playing chess." first presented at the National IRE Convention, March 9, 1949, and also in Claude Elwood Shannon Collected Papers. IEEE Press, 1993. S. 637-656. pdf ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
Allis, Louis Victor. "Searching for solutions in games and artificial intelligence." Wageningen: Ponsen & Looijen, 1994. S. 171. pdf ↩︎
Silver, David, et al. "A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play." Science 362.6419, 2018. S. 1140-1144. pdf ↩︎
Korf, Richard E. "Depth-first iterative-deepening: An optimal admissible tree search." Artificial intelligence 27.1, 1985. S. 97-109. pdf ↩︎
Schaeffer, Jonathan, and Aske Plaat. "New advances in alpha-beta searching." Proceedings of the 1996 ACM 24th annual conference on Computer science. 1996. S. 125 pdf ↩︎
Greenblatt, Richard D., Donald E. Eastlake III, and Stephen D. Crocker. "The Greenblatt chess program." Proceedings of the November 14-16, 1967, fall joint computer conference. 1967. S. 806-807. pdf ↩︎
Zobrist, Albert L. "A new hashing method with application for game playing." ICGA Journal 13.2, 1990. S. 69-73. pdf ↩︎
Berliner, Hans J. "Some Necessary Conditions for a Master Chess Program." IJCAI. Vol. 3. , 1973. pdf ↩︎
Beal, Don F. "A generalised quiescence search algorithm." Artificial Intelligence 43.1, 1990. S. 85-98. pdf ↩︎
Russell, Stuart J., and Peter Norvig. Artificial intelligence a modern approach. London, 2010. S. 169-170 pdf ↩︎ ↩︎
Dendek, Cezary, and Jacek Mandziuk. "A neural network classifier of chess moves." 2008 Eighth International Conference on Hybrid Intelligent Systems. IEEE, 2008. ↩︎
Greer, Kieran. "Computer chess move-ordering schemes using move influence." Artificial Intelligence 120.2, 2000. S. 235-250. ↩︎
Marsland, T. Anthony, and Murray Campbell. "Parallel search of strongly ordered game trees." ACM Computing Surveys (CSUR) 14.4, 1982. S. 533-551. pdf ↩︎
Shams, Reza, Hermann Kaindl, and Helmut Horacek. "Using Aspiration Windows for Minimax Algorithms." IJCAI. 1991. ↩︎
Lai, Matthew. "Giraffe: Using deep reinforcement learning to play chess." arXiv preprint arXiv:1509.01549, 2015. pdf ↩︎ ↩︎ ↩︎ ↩︎
Beal, Donald F., and Martin C. Smith. "Learning piece-square values using temporal differences." ICGA Journal 22.4, 1999. S. 223-235. ↩︎ ↩︎
Droste, Sacha, and Johannes Fürnkranz. "Learning the piece values for three chess variants." ICGA Journal 31.4, 2008. S. 209-233. pdf ↩︎ ↩︎
Kendall, Graham, and Glenn Whitwell. "An evolutionary approach for the tuning of a chess evaluation function using population dynamics." Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat. No. 01TH8546). Vol. 2. IEEE, 2001. S. 996. pdf ↩︎ ↩︎
Chen, Jr-Chang, et al. "Comparison training for computer Chinese chess." IEEE Transactions on Games 12.2, 2019. 169-176. pdf ↩︎ ↩︎
Bošković, B., et al. "History mechanism supported differential evolution for chess evaluation function tuning." Soft Computing 15, 2010. 667-683. html ↩︎ ↩︎
Hauptman, Ami, and Moshe Sipper. "GP-endchess: Using genetic programming to evolve chess endgame players." European Conference on Genetic Programming. Berlin, Heidelberg: Springer Berlin Heidelberg, 2005. S. 120-131. pdf ↩︎
Thrun, Sebastian. "Learning to play the game of chess." Advances in neural information processing systems 7, 1994. pdf ↩︎ ↩︎ ↩︎
Baxter, Jonathan, Andrew Tridgell, and Lex Weaver. "TDLeaf (lambda): Combining temporal difference learning with game-tree search." arXiv preprint cs/9901001, 1999. pdf ↩︎
Nasu, Yu. "Efficiently updatable neural-network-based evaluation functions for computer shogi." The 28th World Computer Shogi Championship Appeal Document 185, 2018. english version pdf ↩︎
Walczak, Steven. "Improving opening book performance through modeling of chess opponents." Proceedings of the 1996 ACM 24th annual conference on Computer science. 1996. pdf ↩︎
Buro, Michael. "Toward opening book learning." ICGA Journal 22.2, 1999. S. 98-102. pdf ↩︎
Peterson, Christopher D. "The effect of endgame tablebases on modern chess engines." 2018. pdf ↩︎