¶ Selektivität
Selektivität ist die Idee, wichtige und interessante Suchbaumzweige, welche mit höherer Wahrscheinlichkeit zur Hauptvariante (Principal Variation) gehören, zu erkennen und tiefer zu suchen, und uninteressante Suchbaumzweige weniger tief zu suchen bzw. gänzlich ungesucht zu lassen.
Um zu ermitteln, welche Zweige interessant bzw. uninteressant sind, werden Heuristiken benutzt. In diesem Kontext redet man von Extensions (Heuristiken nach denen Suchbaumpfade tiefer gesucht werden), Reductions (Heuristiken nach denen Suchbaumpfade weniger tief gesucht werden) und Pruning (Heuristiken nach denen Suchbaumpfade gänzlich ungesucht bleiben). Im Folgenden sind einige gängige Heuristiken aufgeführt:
- Extensions
- Reductions
- Pruning
- Experimente zu Selektivität
¶ Extensions
¶ Check Extension
Bei der Check Extension wird die Suchtiefe um (typischerweise) einen Halbzug erhöht, wenn einer der beiden Spieler im Schach steht. Schachgebene Züge sind sogenannte forcing (dt. zwingende) Züge und stellen eine große Gefahr für den Gegner dar. Die Motivation hinter dieser Extension ist somit, Gewissenheit über den Ausgang einer erzwungenen Variationen zu erlangen und den Horizon Effekt zu verringern. Dadurch, dass die Anzahl der Züge des im schachstehenden Spielers gezwungenermaßen meist sehr gering ist, ist mit keiner Suchexplosion durch die Extension zu rechnen. Trotz der erhöhten Anzahl an untersuchten Knoten erweisen sich Check Extensions als effektive Methode die Spielstärke eines Schachprogrammes zu erhöhen[1].
¶ Singular Extension
Singular Extensions wurden erstmals 1988[2] von Thomas Anantharaman, Murray Campbell und Feng-hsiung Hsu eingeführt. Die Idee der Singular Extension ist es den besten Zug für die Position vertieft (meist um einen Halbzug mehr) zu suchen, wenn dieser wesentlich besser (um eine Marge S) als alle anderen möglichen Züge ist. Offensichtlich wissen wir während der Suche weder (a) was der beste Zug ist noch (b) ob dieser besser als alle anderen möglichen Züge ist. Daher müssen einige Abschätzungen gemacht werden:
- Typischerweise veranschlagt man den besten Zug aus der letzten Iteration der Iterative-Deepening Suche als den wahrscheinlich besten Zug. Dieser ist in der Transposition Table gespeichert. Es kann vorkommen, dass kein bester Zug für die gegebene Position in der Transposition Table vorhanden ist (bspw. wenn die Position nicht in der letzten Iteration untersucht wurde). Dann ist kein Singular Extension möglich.
- Um zu beurteilen, ob dieser Zug wesentlich besser als alle anderen Züge ist, wird eine Vorsuche mit verringerter Tiefe gemacht. Dabei nimmt man die Evaluation des Zuges aus der letzten Iteration und subtrahiert von diesem eine gewisse Marge S. Die Vorsuche wird dann mit einem Alpha-Beta-Fenster verringerter Größe, typischerweise einem Null-Fenster gemacht (siehe Vergleich: PVS-Search.
Stellt sich nun heraus, dass keiner der möglichen Züge besser als der vermeintlich beste Zug abzüglich der Marge S ist, so nimmt man an, dass dieser "beste" Zug tatsächlich wesentlich besser als alle anderen ist, und sucht diesen Suchbaumpfad mit erhöhter Tiefe.
Die ursprüngliche Ausführung (1988) der Singular Extensions konzentrierte sich im Gegensatz zur obigen Beschreibung ausschließlich auf Hauptvarianten-Knoten. Durch die enormen Steigerungen in Hauptspeichergröße und Geschwindigkeit, können heutzutage weitaus mehr als die Hauptvariatenknoten in der Transposition Table gespeichert werden.
In ihrer Arbeit zeigten sie, dass Singular-Extensions signifikante Verbesserungen bewirken konnten. Der Schachrechner gewann damals mit einer überzeugenden Bilanz von 15:5 im Selbstspiel gegen die Version ohne Singular Extensions. Auch heute nutzen Schachprogramme1 noch Singular Extensions.
¶ Reductions
¶ Late Move Reduction
Late Move Reductions[3] basieren auf der Annahme, dass die Zugsortierung in der Alpha-Beta-Suche gut ist, d.h. dass starke Züge als Erstes und schlechtere Züge später untersucht werden. Unter dieser Annahme, reduziert man die Suchtiefe der später untersuchten Züge, da es unwahrscheinlich(er) ist, dass sie anheben (d.h. besser als einer der früheren Züge sind). Ab welcher Anzahl an Zügen und um welche Tiefe die Suchtiefe reduziert wird ist Implementierungsabhängig.
Implementiert werden Late Move Reductions indem starke Züge mit voller Tiefe und vollem Fenster , und die späteren Züge mit reduzierter Tiefe und einer Nullfenster untersucht werden (siehe Vergleich: PVS-Search). Durch die Nullfenstersuche wird (relativ schnell) festgestellt, ob der Zug tatsächlich unterschreitet. Unterschreitet der Zug , so haben wir Zeit in der Suche gespart und fahren mit der Untersuchung des nächsten Zuges fort. Ergibt die Nullfenstersuche jedoch, dass überschritten wurde (der Zug also scheinbar besser als jeden bisher Gesehener ist), so muss eine Suche mit voller Tiefe und vollem Fenster wiederholt werden.
Es hat sich herausgestellt, dass es in manchen Positionen fatal ist Late Move Reductions zu benutzen, bspw. in taktischen Positionen wie im Schach zu stehen oder wenn einer der Spieler einen Bauern umgewandelt hat. Typischerweise wird daher geprüft ob solch eine Position vorliegt, bevor eine LMR amgewandt wird.
Im Folgenden eine (NegaMax-)Implementierung in C:
int search(board_t board, int depth, int alpha, int beta) {
if (depth == 0) {
return eval(board);
}
int searched_moves = 0;
move_t *moves = calculate_moves(board);
move_t best_move;
move_t move;
int eval;
while(move = pop_move(moves)) {
searched_moves++;
do_move(board)
if(searched_moves < REDUCTION_BOUND || !reduction_allowed(board)) {
/* early moves are searched normally */
eval = -search(board, depth-1, -beta, -alpha);
} else {
/* late moves (where reduction is allowed) are searched */
/* with a reduced depth null-window search */
eval = -search(board, depth-1-REDUCTION_FACTOR, -(alpha +1), -alpha);
/* costly research */
if (eval >= alpha) {
eval = -search(board, depth-1, -beta, -alpha);
}
}
undo_move(board);
/* normal alpha beta stuff */
if (eval > alpha) {
alpha = eval;
best_move = move;
}
if (alpha >= beta) {
break
}
}
return alpha;
}
¶ Null Move Reduction
Null Move Reduction ist sehr ähnlich zu Null Move Pruning. Für die grundlegende Idee siehe hier. Anstatt Suchbaumpfade bei Erfüllen der Bedingung für Null Move Pruning abzuschneiden, wird hier stattdessen die Suchtiefe stark reduziert, typischerweise um 4 Halbzüge. Dies hat den Vorteil, dass das Schachprogramm trotz einer (zeitintensiveren) erneuten Suche, nicht so anfällig gegenüber Positionen ist, bei denen die Null Move Observation nicht zutrifft, dies jedoch im Voraus nicht erkannt wird[4].
Im Folgenden sind die Anpassungen an der Implementierung von NMP in C zu NMR:
int search(board_t board, int depth, int alpha, int beta) {
if (depth == 0) {
return eval(board);
}
if (null_move_allowed()) {
do_null_move(board);
eval = -search(board, depth - 1 - REDUCTION_FACTOR, -beta, -beta + 1);
undo_null_move(board);
if (eval >= beta) {
/* to NOT return beta */
/* but rather reduce the depth */
depth -= 4
}
}
/* and continue search ... */
}
¶ Pruning
¶ Futility Pruning
Beim Futility Pruning[3:1] wird Pruning an den Knoten der "vorletzten" Tiefe vollzogen (in der Suche sind dies die Knoten, bei denen depth == 1).
¶ Vorwissen
In einer Suche ohne Futility Pruning, erfolgen normerweise drei Schritte um eine Evalution für einen Knoten zu erhalten.
- Der betrachtete Zug wird mit einer
do_move()Funktion ausgeführt - Die Suche ruft sich rekursiv auf
eval = search(depth - 1) - Nachdem der Zug (durch den rekursiven Aufruf) evaluiert wurde, wird der Zug mit einer
undo_move()Funktion zurückgenommen
Es fällt nun auf, dass der rekursive Aufruf von search(depth - 1) an solchen "vorletzten" Knoten dazu führt, dass aufgrund der Abbruchbedingung (depth == 0) direkt eine Evaluation durchgeführt und das Ergebnis zurückgegeben wird.
¶ Idee
Die Grundidee von Futility Pruning besteht darin, die Aufrufe von do_move(), search(depth - 1), und undo_move() zu vermeiden, indem eine Vorevaluation des Zuges durchgeführt wird. Wenn diese Vorevaluation abzüglich einer Sicherheitsmarge ergibt, dass der Zug den Wert nicht erhöhen kann – d.h. der Zug schlechter ist als alle zuvor betrachteten Züge – dann werden die oben genannten Aufrufe eingespart, und der Suchbaum bereits an diesem Knoten abgeschnitten.
Die Vorevaluation ist in der Regel wesentlich einfacher gestaltet als die vollständige Evaluation, was den zusätzlichen Vorteil weiterer Zeitersparnis bietet. Als Sicherheitsmarge wird oft der größtmögliche Fehler der Vorevaluation zur tatsächlichen Evaluation verwendet.
In einem Beispiel für einen Schachrechner, der für seine Evaluation materielle und positionelle Vorteile berücksichtigt, könnte die Vorevaluation darauf abzielen, grob zu bestimmen, ob der Zug wahrscheinlich signifikante Verbesserungen in Bezug auf Materialgewinn bringt und als Sicherheistmarge könnte der größtmögliche positionelle Vorteil benutzt werden.
Es hat sich herausgestellt, dass es in einigen Positionen problematisch ist, Futility Pruning zu verwenden, insbesondere in taktischen Positionen wie wenn einer der Spieler im Schach steht oder einen Bauern umgewandelt hat. Daher wird üblicherweise überprüft, ob sich eine solche Position ergibt, bevor Futility Pruning angewendet wird.
Im Folgenden eine (NegaMax-)Implementierung in C:
int search(board_t board, int depth, int alpha, int beta) {
if (depth == 0) {
return eval(board);
}
move_t *moves = calculate_moves(board);
move_t best_move;
move_t move;
int eval;
while(move = pop_move(moves)) {
do_move(board)
if (preeval(board) + FUTILITY_MARGIN <= alpha && futility_allowed()){
continue
}
eval = -search(board, depth-1, -beta, -alpha);
undo_move(board);
/* normal alpha beta stuff */
if (eval > alpha) {
alpha = eval;
best_move = move;
}
if (alpha >= beta) {
break
}
}
return alpha;
}
¶ Null Move Pruning
Null Move Pruning[3:2] basiert auf der Null Move Observation, die besagt, dass es (oft) besser ist einen Zug zu machen, als einen Zug auszulassen und den Gegner zwei Mal spielen zu lassen.
Beim Null Move Pruning wird ein Null Move durchgeführt, das heißt, der eigene Zug übersprungen, und eine tiefenreduzierte Nullfenstersuche vollzogen. Dabei wird überprüft, ob der Gegner trotz des eigens "verpassten" Zuges nicht in der Lage ist, seine Position zu verbessern. Falls der Gegner seine Position nicht verbessern kann (d.h. wurde in der tiefereduzierten Suche überschritten - es wäre zu einem Beta-Cutoff gekommen), dann wird der Zweig abgeschnitten, da anzunehmen ist, dass es auch in der vollen Tiefe ohne Null Move zu einem Beta-Cutoff gekommen wäre. Der Gegner hätte diesen Zweig nicht gewählt hätte, da man selber "zu gut" ist. Wird bei der Nullfenstersuche jedoch unterschritten, so muss die Suche mit voller Tiefe und vollem Fenster wiederholt werden.
Beim Null Move Pruning müssen einige Punkte beachtet werden. Null Move Pruning ist nicht zulässig, wenn der der betrachtete Spieler im Schach steht, da hier ein Null Move in einer illegalen Position enden würde. Des Weiteren sind zwei aufeinanderfolgende Null Moves nicht erlaubt (eher nicht erwünscht), da dies keine Auswirkungen hätte. Außerdem basiert Null Move Pruning auf der Annahme, dass die Null Move Observation gilt. Es gibt jedoch Positionen, sogenannte "Zugzwang"-Positionen, in denen es besser wäre, keinen Zug zu machen. Solche Positionen treten insbesondere in den Endspielphasen auf, weshalb es sinnvoll sein kann Null Move Pruning in diesen Phasen zu deaktivieren.
Der Reduktionsfaktor beträgt in der Regel 2-3 Halbzüge. Einige Schachprogramme sind konservativer und reduzieren nur um 2, während andere aggressiver sind und die Suchtiefe stark reduzieren. Es ist auch möglich, eine Kombination zu verwenden, bei der die Reduktion bei geringen Suchtiefen gering und bei hohen Suchtiefen hoch ist.
Im Folgenden eine (NegaMax-)Implementierung in C:
int search(board_t board, int depth, int alpha, int beta) {
if (depth == 0) {
return eval(board);
}
if (null_move_allowed()) {
do_null_move(board);
eval = -search(board, depth - 1 - REDUCTION_FACTOR, -beta, -beta + 1);
undo_null_move(board);
if (eval >= beta) {
return beta;
}
}
/* normal alpha beta stuff */
move_t *moves = calculate_moves(board);
move_t best_move;
move_t move;
int eval;
while ((move = pop_move(moves))) {
do_move(board, move);
eval = -search(board, depth - 1, -beta, -alpha);
undo_move(board);
if (eval > alpha) {
alpha = eval;
best_move = move;
}
if (alpha >= beta) {
break;
}
}
return alpha;
}
¶ Experimente zu Selektivität
Im Vergleich zur der enormen Anzahl an Heuristiken und Varianten im Bereich der Schachprogrammierung existieren vergleichsweise wenig fundierte Studien zu den Effekten einzelner Techniken. Die Schachprogrammierung bildet eine recht umfangreiche und aktive Sphäre. Es existieren zahlreiche Schachrechner, von denen einige, etwa 500, auf der Computer Chess Ranking List zu finden sind. Die Wirksamkeit einer Technik wird daher nicht nur durch isolierten Studien, sondern auch durch ihre In- oder Exklusion in modernen und leistungsstarken Schachprogrammen belegt.
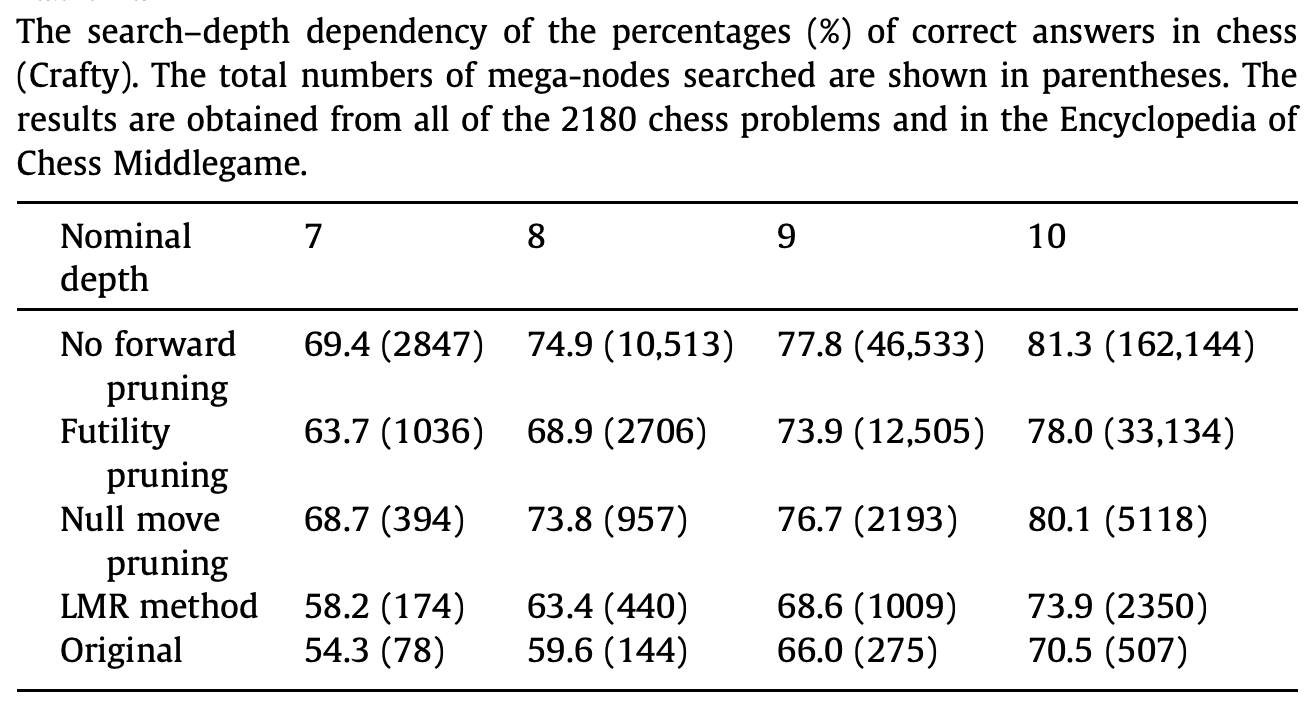
Im Paper "Efficiency of three forward-pruning techniques in shogi: Futility pruning, null-move pruning, and Late Move Reduction (LMR)"[3:3] aus dem Jahr 2012 wurden einige forward-pruning Techniken systematisch untersucht. Die Grafik in Abbildung 1 zeigt die Ergebnisse. Insgesamt zeigen die Resultate, dass die Techniken die Suche zwar ungenauer machen, jedoch erheblich an Berechnungszeit einsparen. Das Schach- und Testprogramm Crafty2 verwendet darüber hinaus sogar weitere Techniken, die ebenfalls zu einer zusätzlichen Ersparnis an Berechnungszeit führen. Trotz der verringerten Genauigkeit in den Zügen setzen Schachrechner auf diese Techniken. Der Grund dafür, wie der Autor in seiner Arbeit andeutet, liegt darin, dass durch die eingesparte Rechenzeit eine tiefere Suche möglich wird, wodurch anfängliche Ungenauigkeiten in flacheren Suchen wieder ausgeglichen werden können.
¶ Fußnoten
1 Wie z.B. Berserk, Carp und Blunder
2 Crafty liegt Stand Januar 2024 mit 3041 ELO weit über dem besten Schachspieler der Welt, Magnus Carlsen, mit 2830 ELO
¶ Referenzen
Ye, Chun, and T. A. Marsland. "Selective Extensions in Game-Tree Search." Heuristic Programming in Artificial Intelligence 3, 1992. S. 112-122. pdf ↩︎
Anantharaman, Thomas, Murray Campbell, and Feng-hsiung Hsu. "Singular extensions: Adding selectivity to brute-force searching." ICGA Journal 11.4, 1988. S. 135-143. pdf ↩︎
Hoki, Kunihito, and Masakazu Muramatsu. "Efficiency of three forward-pruning techniques in shogi: Futility pruning, null-move pruning, and Late Move Reduction (LMR)." Entertainment Computing 3.3, 2012. 51-57. pdf ↩︎ ↩︎ ↩︎ ↩︎
David-Tabibi, Omid, and Nathan S. Netanyahu. "Extended null-move reductions." International Conference on Computers and Games. Berlin, Heidelberg: Springer Berlin Heidelberg, 2008. pdf ↩︎