¶ Entstehung

Arimaa ist ein 2-spieler Brettspiel mit perfekter Information, welches von dem Informatiker Omar Syed entwickelt und im Jahr 2002 veröffentlicht wurde. Syed war vom Sieg des Schachcomputers Deep Blue gegen den damaligen Schachweltmeister Garry Kasparov inspiriert und entwarf das Spiel mit den Hintergedanken, dass es schwierig für Computer zu spielen sein soll, aber simpel genug für seinen vierjährigen Sohn Aarmir. Sein Sohn inspirierte auch den Namen des Spiels: Das Wort Arimaa ist Aarmir rückwärts geschrieben mit einem zusätzlichen A am Anfang. [1]
¶ Arimaa Challenge
Von 2004 bis 2015 fand jährlich die Arimaa Challenge statt, bei welcher menschliche Spieler gegen Computerprogramme in Arimaa antraten. Syed schrieb für die Entwickler des ersten siegreichen Programmes ein Preisgeld von 10.000 $ aus. Das Ziel der Challenge war es die Entwicklung von Algorithmen für komplexe Spiele zu fördern und neue Techniken und Lösungsansätze zu entdecken. [2]
Im Jahr 2015 gewann erstmalig ein Programm namens Sharp die Challenge, womit heutzutage auch in Arimaa die besten Spieler Computer sind.
¶ Spielregeln
Arimaa wird von 2 Spielern (Gold und Silber) auf einem normalen Sachbrett gespielt, wobei die Felder c3, f3, c6 und f6 zusätzlich als Fallen gekennzeichnet sind. Jeder Spieler hat als Spielfiguren:
- 1 Elefant
- 1 Kamel
- 2 Pferde
- 2 Hunde
- 2 Katzen
- 8 Kaninchen
wobei die Figuren hier absteigend nach ihrer Stärke angeordnet sind.
Das Spiel beginnt damit, dass der goldene Spieler seine Figuren beliebig auf den ersten beiden Reihen platziert. Im Anschluss postiert Silber seine Figuren auf den letzten beiden Reihen in beliebiger Anordnung.

Nun spielen beide Spieler abwechselnd jeweils einen Zug, wobei Gold beginnt. Ein Zug besteht hierbei aus mindestens einem und maximal vier Schritten, wobei in jedem Schritt eine der eigenen Spielfiguren auf ein freies, orthogonal anliegendes Feld bewegt wird. Alle Figuren besitzen somit die gleichen Bewegungsmöglichkeiten. Die einzige Ausnahme sind die Kaninchen, welche als einzige Figuren nicht nach hinten bewegt werden dürfen.
¶ Fangen und Schieben
Alternativ können innerhalb eines Zuges zwei Schritte verbraucht werden, um eine schwächere Figur des anderen Spielers auf einem orthogonal benachbarten Feld zu vertreiben. Hierbei zählen das Bewegen der gegnerischen sowie der eigenen Figur als jeweils ein Schritt. Es gibt zwei Arten der Vertreibung:
- Das Ziehen - Man bewegt seine Figur auf ein anliegendes, leeres Feld und bewegt die schwächere Gegnerfigur in das freigewordene Feld.
- Das Schieben - Man bewegt die schwächere Gegnerfigur auf ein anliegendes, leeres Feld und zieht die eigene Figur in das freigewordene Feld nach.
Es ist nicht möglich, mit einer Figur gleichzeitig zu schieben und zu ziehen.

¶ Festhalten und Fangen
Zusätzlich gibt es Einschränkungen, wann man eine Figur bewegen darf. Ein Spieler darf innerhalb eines Schrittes eine seiner eigenen Figuren nicht bewegen, wenn diese Figur festgehalten wird. Eine Figur wird festgehalten, wenn eine stärkere Figur des Gegners orthogonal benachbart zu dieser ist, aber keine weitere eigene Spielfigur.
Darüber hinaus muss ein Zug eine Änderung der Spielposition erzeugen. Die entstandene Position darf zudem maximal zweimal im vorherigen Spielverlauf vorgekommen sein.
Befindet sich innerhalb eines Zuges eine Figur auf einer Falle, ohne dass eine weitere Figur desselben Spielers an dieser Falle angrenzt, wird diese Figur gefangen und aus dem Spiel entfernt. Insbesondere kann man also gegnerische Figuren geschickt in Fallen schieben oder sogar ziehen und diese damit gefangen nehmen.
¶ Spielende
Es gibt drei Möglichkeiten, wie eine Partie enden kann:
- Einer der Spieler schafft es, eines seiner Kaninchen ans andere Ende des Spielbrettes zu bewegen. Befindet sich ein Kaninchen am Ende eines Zuges auf der jeweils gegenüberliegenden Seite, gewinnt damit der jeweilige Spieler. Das ist das Hauptziel des Spieles und die häufigste Art, wie Runden enden.
- Wenn ein Spieler alle Kaninchen des Gegners gefangen nimmt, gewinnt er - selbst wenn er dabei im letzten Zuge sein eigenes letztes Kaninchen verliert.
- Kann ein Spieler keinen legalen Zug ausführen, verliert dieser Spieler.
Damit enden alle Arimaa-Partien in einem Sieg von einem der Spieler und es gibt kein Unentschieden.
¶ Beispiel
Betrachten wir folgendes Beispiel[3], um einen möglichen Zug nachzuvollziehen:
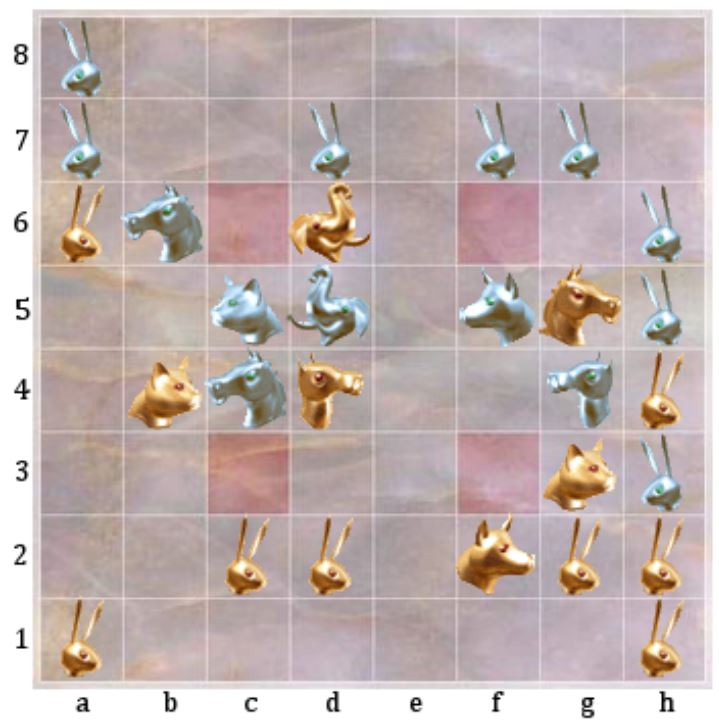
Gold ist in dieser Situation am Zuge und muss Folgendes beachten:
- Silber ist im nächsten Zug in der Lage, das Pferd auf g5 gefangen zu nehmen, indem das Kamel auf g4 genutzt wird, um durch zweifaches Schieben das Pferd auf die unbeschützte Falle f6 zu manövrieren.
- Gold kann das silberne Pferd auf c4 gefangen nehmen, indem das Kamel auf d4 dieses verschiebt. Das Kamel wird jedoch von dem Elefanten auf d5 festgehalten.
Ein möglicher Zug wäre nun das Kaninchen von d2 nach d3 zu bewegen, wodurch das Kamel auf d4 nicht mehr festgehalten wird, anschließend das Pferd mit dem Kamel auf c3 zu schieben, also gefangen zu nehmen und letztlich den Elefanten von d6 nach e6 zu bewegen, wodurch das goldene Pferd nicht mehr auf f6 gefangen werden kann.
¶ Algorithmische Lösungsansätze
Da Arimaa als möglichst computerresitentes Spiel konzipiert wurde, ist es sinnvoll zunächst zu analysieren, welche Aspekte das Spiel im Vergleich schwer lösbar machen. Beispielsweise ist es für Menschen keineswegs schwieriger zu erlernen als Schach und kann sogar mit den gleichen Materialien gespielt werden (repräsentiere Elefanten durch Könige, Kamele durch Damen etc.), wird aber erst seit 2015 von Computern besser gespielt als von menschlichen Spielern, obwohl das bei Schach schon weitaus früher der Fall war und es durch die Arimaa-challenge durchaus einige Versuche gab, starke Programme zu entwickeln.
¶ Gründe für die anfängliche Computerresitenz
Einer der Gründe dafür ist, dass die Spieler ihre Figuren zu Beginn des Spieles beliebig auf den ersten/letzten zwei Reihen (also 16 Feldern) platzieren. Berücksichtigt man die Anzahlen an Figuren der verschiedenen Arten ergeben sich somit
Möglichkeiten pro Spieler seine Figuren aufzustellen. Insgesamt gibt es also Anfangspositionen bei Arimaa. [4] Damit sind Eröffnungsdatenbanken, welche bei Spielen mit festem Anfangszustand wie beispielsweise Schach sehr gut funktionieren, bei Arimaa in der Praxis eher nutzlos. Ein ähnliches Problem gibt es bei Endspieldatenbanken. In den meisten Fällen enden Arimaa-Runden nämlich mit (fast) allen Figuren noch auf dem Spielbrett. Daher ist der Nutzen solcher Datenbanken bei Arimaa stark begrenzt. [5]
Darüber hinaus hat Arimaa einen hohen durchschnittlichen Verzweigungsgrad, sprich eine große Anzahl an verschiedenen möglichen Zügen. Dadurch gibt es sehr viele verschiedene Spielverläufe, selbst wenn die absolute Anzahl verschiedener Positionen im Spiel vergleichbar zu Spielen wie Schach ist. Der Sachverhalt ist in der folgenden Tabelle verdeutlicht:
| Spiel | Anzahl Positionen | Verzweigungsgrad | Anzahl Spielverläufe | |
|---|---|---|---|---|
| Schach | ||||
| Go | ||||
| Arimaa | ||||
Tabelle 1: Vergleich Spielkomplexität bei Schach, Go und Arimaa [3:1]
Der Verzweigungsgrad wurde hier aus dem Durchschnitt einer Arimaa Spieledatenbank errechnet. Andere Quellen mit einer unterschiedlichen Datenbank geben einen teilweise höheren Verzweigungsgrad an. [6] Hierbei muss jedoch auch berücksichtigt werden, ob verschiedene Schrittreihenfolgen, die praktisch den selben Zug bilden, doppelt gezählt werden. Bei dem Wert in der Tabelle werden diese nur ein mal gezählt. [3:2]
Der hohe Verzweigungsgrad des Spiels lässt vermuten, dass klassische Suchalgorithmen wenig erfolgversprechend für einen effizienten Arimaa-Bot sind. In der Praxis sind diese durch einige Anpassungen jedoch inzwischen ziemlich erfolgreich.
¶ MCTS für Arimaa
Die ersten Arimaa-Programme nutzten ähnliche Ansätze wie damalige Schachprogramme, insesondere die Alpha-Beta Suche. Da Monte-Carlo-Tree Search (MCTS) in Spielen wie Go, Amazons und Hex gute Erfolge erzielen konnte, implementierte Tomás Kozelek MCTS auch für Arimaa. Die Ergebnisse waren dabei jedoch ernüchternd. Der Standardalgorithmus erreichte nur eine schlechte performance und selbst mit einigen Verbesserungen, konnte MCTS nur mit mittelmäßigen Alpha-Beta Programmen mithalten. [5:1] Als Grund nennt Kozelek mitunter die Stärke von Evaluierungsfunktionen für Arimaa, auf welche Alpha-Beta Programme zurückgreifen. [5:2]
¶ Alpha-Beta Suche für Arimaa
2015 gelang schließlich David J. Wu der Durchbruch und sein Programm Sharp gewann die Arimaa-Challenge. Sharp benutzt, wie die meisten Arimaa-Programme, eine Alpha-Beta Suche um den Spielbaum nach einem möglichst starken Spielzug zu durchsuchen. Aufgrund des enormen Verzweigungsgrades reicht eine Standardimplementation des Algorithmus nicht aus um guten menschlichen Spielern Konkurrenz zu machen. Daher greift Sharp auf einige Anpassungen und Erweiterungen zurück: [7]
- Hybride Formulierung der Suche
- Iterative Tiefensuche
- Transpositionstabllen
- Ruhesuche
- Verschiedene Techniken für Zugsortierung
- Suchtiefenreduktion
¶ Hybride Formulierung der Suche
Da Züge in Arimaa aus bis zu vier Schritten bestehen, gibt es zwei Möglichkeiten die Suche durchzuführen:
- Es werden "klassisch" Züge für die Suche betrachtet. Das heißt, in jedem Rekursionslevel der Suche wechselt der Spieler und es werden durchschnittlich ca. 16.000 Züge generiert und sortiert (siehe Zugsortierung)
- Die Suche betrachtet Schritte anstelle von Zügen, wodurch der Verzweigunsgrad drastisch auf ca. 30 sinkt. [7:1] Der Spieler wechselt alle vier Rekursionsebenen.
Die Vorteile der zweiten Variante entstehen durch den geringeren Verzweigungsgrad. So kann es in der ersten Variante passieren, dass tausende Züge generiert werden, nur damit ein anschließender Cutoff die Suche an diesem Knoten beendet. Zudem lassen sich kleinere Listen an Zügen schneller sortieren (siehe Zugsortierung). Problematisch ist jedoch, dass diese Formulierung dazu führt, dass ein potentiell vielversprechender Zug, dessen erster Schritt jedoch keine weiteren guten Züge ermöglicht, durch die Zugsortierung zu Beginn der Suche betrachtet wird und durch den Tiefensuchencharakter von Alpha-Beta anschließend alle anderen (schlechten) Züge, die mit demselben Schritt beginnen, untersucht werden. Dadurch sinkt die Effektivität der Zugsortierung. [7:2]
Sharp nutzt daher eine neue hybride Formulierung, bei welcher Züge mit bis zu vier Schritten generiert werden, die wiederum die Suchtiefe proportional zu ihrer Länge verringern. Diese Umstellung beschleunigte tiefe Suchen um mehr als 20%. [7:3] Der Grund hierfür wird bei Betrachtung der genutzten Zugsortierung klar (siehe Abschnitt Zugsortierung).
¶ Iterative Tiefensuche
In der Praxis treten die Computerprogramme gegen Menschen bzw. andere Programme in einem zeitbeschränkten Format (beispielsweise eine Minute pro Zug) an. Um die vorhandene Zeit vollständig zu nutzen ohne das Zeitlimit zu überschreiten, verwendet Sharp einen iterativen Ansatz, bei welchem eine Position mehrfach und mit steigender Suchtiefe untersucht wird, bis die Zeit ausläuft. [7:4] Das ist notwendig, da Alpha-Beta Suche zuerst in die Tiefe geht, womit eine einzelne Suche bis zum Zeitlimit vermutlich nicht alle Züge betrachten kann.
iterativeSuche(Zeitlimit, Position):
Tiefe = 1
Solange das Zeitlimit nicht abgelaufen ist:
besterZug = alphaBeta(Position, Tiefe, Zeitlimit)
Tiefe += 1
return besterZug
Wenn die Suche bei Erreichen des Zeitlimits abgebrochen wird, nutzt Sharp das Ergebnis der beendeten Suche. Denn wird ein Zug gefunden, der besser ist als der erste Zug, ist dieser durch die Zugsortierung (siehe Abschnitt Zugsortierung) auch stärker als der beste Zug der vorherigen Suche. [7:5]
¶ Transpositionstabellen
Sharp nutzt zudem Transposition tables, um bereits gesehene Positionen und deren Werte für die Suche zu speichern. [7:6] Dies ist auch für die Zugsortierung relevant (siehe Abschnitt Zugsortierung).
¶ Ruhesuche
Ein Problem von tiefenbeschränkter Alpha-Beta Suche ist der Horizonteffekt, welcher Fehleinschätzungen beschreibt, die durch den limitierten Suchraum entstehen. Zum Beispiel kann es auftreten, dass zur Niederlage führende Positionen sehr gut bewertet werden, da die entscheidenden Züge, welche letztlich den Verlust forcieren, nicht mehr untersucht werden. Um diesen Effekt zu minimieren, setzen viele Alpha-Beta Programme auf eine Ruhesuche, bei welcher "instabile" Positionen über die eigentliche Tiefe hinaus untersucht werden. [8]

Sharp verwendet aufgrund des hohen Verzweigungsgrades eine Ruhesuche von maximal 12 Schritten, wobei fangende Züge (Züge, durch welche eine Figur gefangen wird), das Schieben und Ziehen von fallenverteidigenden Figuren sowie einige weitere Züge durchsucht werden. [7:7]
¶ Zugsortierung
Eine der potentiell stärksten Anpassung für Alpha-Beta Programme ist die Implementierung verschiedener Mechanismen zur Zugsortierung. Eine Zugsortierung wird oft genutzt, um die Reihenfolge, in welcher Züge untersucht werden, festzulegen. Das liegt daran, dass wenn bessere Züge zuerst untersucht werden, mehr Cutoffs auftreten, was eine tiefere Suche ermöglicht. Darüber hinaus können bei einer ausreichend starken Sortierung zusätzliche Cutoffs eingesetzt werden, indem man die schwächsten Züge ignoriert, oder deren Suchtiefe verringert (siehe Suchtiefenreduktion).
Sharp greift auf zwei verschiedene Varianten der Zugsortierung zurück. Im Wurzelknoten kommt eine spezielle Sortierung, die auf einem Bradley-Terry Modell basiert, zum Einsatz. Innerhalb des Suchbaumes werden schnellere Heuristiken sowie die Transposition Table genutzt. [7:8]
¶ Im Wurzelknoten
Das Ziel des Bradley-Terry Modells ist es eine Zugsortierungsfunktion zu finden, welche möglichst genau den besten Zug vorhersagt. Formal seien
- die Menge der Spielzustände
- alle möglichen Züge
- alle möglichen Züge in Zustand
Mit jedem Zustand und Zug assoziieren wir nun einen Vektor binärer Eigenschaften, fortan features, . Die features erlauben eine feinere Differenzierung zwischen scheinbar ähnlichen Zügen und insbesondere eine Verallgemeinerung über verschiedene Position, da man Trends erkennen kann, welche features gute Züge ausmachen. [3:3] Dazu mehr in den nächsten Paragraphen. Sharp nutzt beispielsweise [3:4]
- 512 features um den Status der Fallen zu kodieren
- 256 features um auszudrücken, dass Bedrohungen einer eigenen Figur entfernt werden
- 6 features für Goal Threats, also die Möglichkeit das Spiel zu gewinnen/verlieren.
Die features kodieren also intuitiv die Auswirkungen eines Zuges auf vermutlich relevante Stellungen/Strukturen der Spielposition.
Das Ziel ist es nun für Trainingsinstanzen , wobei den möglichen Zügen und dem besten Zug entspricht, eine Funktion zu finden, sodass den Vektor zum besten Zug in zukünftigen Spielen möglichst hoch ordnet (durch eine Ordnung über den Vektoren, wobei ).[3:5]
Da der optimale Zug in der Praxis nicht immer bestimmt werden kann, wurden in der Trainingsphase "Expertenzüge", also ein von einem starken menschlichen Spieler gespielte Züge, genutzt.[3:6] In anderen Worten soll das Modell also möglichst genau vorhersagen, welchen Zug ein menschlicher Experte spielen würde. Gesucht ist also eine Funktion, welche die Stärke von Zügen in einem Zustand anhand ihrer features bewertet. Diese Funktion soll dabei aus den gegebenen Trainingsinstanzen erlernt werden.
Ein Bradley-Terry Modell beschreibt die Wahrscheinlichkeit von Ausgängen paarweiser Vergleiche von Individuen einer Gruppe wie folgt: [9]
wobei als "Individuum i schlägt Individuum j" verstanden wird und die "Stärke" des jeweiligen Individuums beschreibt. Beispielsweise könnten die einzelnen Individuen Sportler darstellen, wobei das Modell dann die Gewinnchance eines Sportlers gegen einen anderen beschreibt.
Für eine Menge bzw. ein Team an Individuen lässt sich nun verallgemeinert durch
die Stärke eines Teams und somit bei Vergleich von Teams die Gewinnchance für
definieren. [3:7] Für die Zugsortierung von Sharp ist nun jedes feature ein Individuum des Modells mit zunächst unbekannter Stärke . Jeder Zugvektor wird dann als Team seiner features verstanden mit Stärke .[3:8] beschreibt hierbei den Wert von feature in . Die Stärke eines Zuges setzt sich demnach direkt aus der Stärke seiner vorhandenen features zusammen. Um den Expertenzug in Zustand vorherzusagen, ergibt sich die Ordnungsfunktion
bzw. ohne den redundanten Nenner. Die Parameter wurden durch Maximum-a-positeriori-Schätzung mit 4121 Spielen als Trainingsinstanzen erlernt.[3:9]
Die Zugsortierung wird also als Wettbewerb zwischen den Zügen modelliert, wobei der Zug, welcher am wahrscheinlichsten "gewinnt", sprich dem Expertenzug gleicht, als bester Zug angesehen wird. Genauer gesagt, findet ein Wettkampf zwischen Teams an features statt. Das Ergebnis kann also so verstanden werden, dass das die beste Bündelung an konkreten Auswirkungen auf den aktuellen Zustand (über das reine Bewegen der jeweiligen Figuren im Zuge hinaus) gewinnt. Da jedem feature eine Stärke zugewiesen wird, kann man daran theoretisch auch ablesen, welche features am relevantesten sind, sprich was einen guten Zug ausmacht.
Die Sortierung wurde an 439 Spielen als Testinstanzen getestet, wobei fast 90% der Expertenzüge innerhalb der ersten 5% Züge der entsprechenden Sortierung landeten. [3:10] In folgender Tabelle sind die genauen Werte für verschiedene Prozentbereiche abgebildet:
| Top X Prozent | 5% | 10% | 20% | 40% | 60% | 80% | ||
|---|---|---|---|---|---|---|---|---|
| Prozent der Züge | 89.4 | 94.3 | 97.7 | 99.3 | 99.7 | 99.9 | ||
Tabelle 2: Anteil der Expertenzüge innerhalb der besten X Prozent Züge laut Zugsortierung. Übernommen aus [3:11].
Obwohl die Sortierung an sich nach ihrer Implementierung interessanterweise keinen Vorteil gegenüber einer früheren Version von Sharp ohne Bradley-Terry Modell ergab, erlaubt sie effektives abschneiden von schlechten Zügen, weit hinten in der Sortierung, wodurch signifikate Verbesserung im Spielverhalten entstanden. [3:12]
In der neusten Version wird bei allen außer den ersten 10% der Züge jedoch nur die Tiefe der Suche reduziert, was aber bereits große Beschleunigungen der Suche mit sich trägt (siehe Reduktion der Suchtiefe). [7:9]
Als potentielle Gründe dafür, dass die Sortierung an sich keinen Vorteil erbrachte, nennt Wu unter anderem, dass die zum Vergleich genutzte Version bereits eine Art Zugsortierung nutzt und die Möglichkeit, dass das Zeitlimit zu niedrig war, um die Vorteile der reinen Zugsortierung zu bemerken. [3:13]
¶ Innerhalb des Suchbaums
Die Sortierungsfunktion des Wurzelknotes ist in der Praxis zu langsam, um sie innerhalb des Suchbaumes zu verwenden. [7:10] Die Zugsortierung erfolgt daher durch das Anwenden schneller Heuristiken und generiert die Züge folgendermaßen: [7:11]
- Der Zug aus der Transposition Table, wenn vorhanden
- Killer Züge
- Fangende Züge
- Taktische Züge
- Schritt eins des Transposition Table Zuges
- Alle weiteren Schritte sowie schiebende/ziehende Züge
Hier ist auch der Vorteil der hybriden Formulierung der Suche erkennbar. Die vielversprechensden Züge werden auch als solche innerhalb eines Rekursionsschrittes untersucht ohne die Suche zu zwingen alle weiteren Züge, die mit demselben Anfangsschritt beginnen, zu betrachten. Gleichzeitig bleibt der Verzweigungsgrad und somit der Aufwand für das Generieren und ordnen der Schritte/Züge überschaubar.
Die Killer Züge entstammen hierbei der Killer Heuristik, welche oftmals bei Alpha-Beta Programmen für Spiele eingesetzt wird. Dabei wird innerhalb jeder Rekursionsebene eine Liste erstellt, welche Züge der nächsten Rekursionsebene enthält, die zu einem Cutoff führten. Diese Züge werden dann mitunter als erste untersucht, mit der Idee, dass starke Gegenzüge auch in anderen Situationen starke Züge darstellen. [8:1] In der Praxis wird also beim Auftreten eines Cutoffs der jeweilige Zug gespeichert. Durch die hybride Suchformulierung müssen bei Sharp die vollen Schritte des Zuges meistens allerdings etwas aufwändiger rekonsturiert werden, da diese über mehrere Rekursionsebenen ausgespielt werden. Es werden dann bis zu 8 Killer Züge nach dem FIFO-Prinzip gespeichert. [7:12]
Das Generieren der "fangenden" Züge, also von Zügen, welche das Fangen einer gegnerischen Figur erlauben, stellt eine Herausforderung dar. Da Züge aus bis zu vier Schritten bestehen, ist es nicht trivial zu überprüfen, welche Züge dies ermöglichen (das gleiche gilt tatsächlich auch, um zu überprüfen, ob ein Zug das Spiel gewinnt). Man könnte eine Suche über vier Schritte ausführen bzw. alle möglichen Züge generieren und testen ob diese eine Figur gefangen nehmen. Das wäre jedoch offensichtlich wenig sinnvoll für die Verwendung innerhalb einer Zugsortierung, insbesondere mit der hybriden Suche. Gute Arimaa-Programme, inklusive Sharp, nutzen daher spezialisierten Code, in welchem direkt Muster, die zu einem solchen Zug führen, geprüft werden. [7:13] Auf diese Art müssen nicht erst Züge generiert, ausgespielt und retrospektiv untersucht werden. Muster dieser Art können beispielsweise durch Entscheidungsbäume erkannt werden:
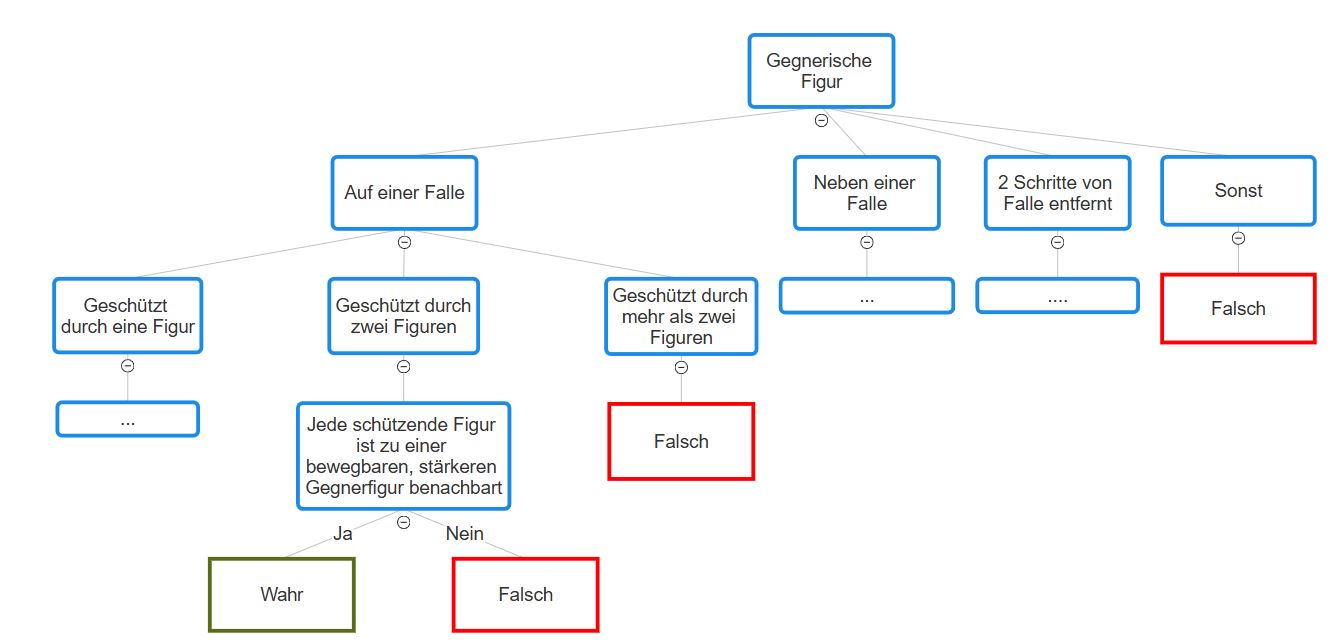
Der vierte Schritt (die Generierung der taktischen Züge) ist das Pendant zu dem Bradley-Terry Modell im Wurzelknoten. Der Hintergrundgedanke ist es, effizient eine geringe Anzahl Züge zu generieren, welche möglichst viele entscheidenden Züge abdecken. [7:14] Ähnlich zu den fangenden Zügen werden dafür direkte Muster gesucht, um zu vermeiden, dass wie im Wurzelknoten die Züge erst ausgespielt und anschließend verglichen werden. Dafür werden unter anderem folgende Klassen an Zügen generiert: [7:15]
- Ziehen und Schieben von Gegnerfiguren, welche benachbart zu einer Falle sind
- Züge, welche Figuren neben Fallen platzieren, die noch nicht gut geschützt sind
- Züge, die starke gegnerische Figuren festhalten
Um die Anzahl generierter Züge zu minimieren, wurden die Generatoren darauf optimiert, die Differenz zwischen der Bewertung des besten generierten Zuges und des Expertenzuges zu minimieren, anstatt möglichst oft den Expertenzug zu generieren. Oftmals sind die Expertenzüge nämlich eher "stille" Züge ohne direkte Konfrontation, weshalb die Generatoren sonst sehr umfassend sein müssten, um diese häufig abzudecken. [7:16]
¶ Reduktion der Suchtiefe
Einer der Vorteile der Zugsortierung ist das potentiell vermehrte Auftreten von Cutoffs. Darüber hinaus kann man bei einer starken Zugsortierung davon ausgehen, dass die Züge hinten in der Sortierung vermutlich keinen Einfluss auf den - bzw. -Wert haben. Man könnte diese Züge also schlichtweg durch einen zusätzlich Cutoff ignorieren.
Um potentielle Fehler, welche durch das komplette Abschneiden von Zügen entstehen können, zu vermeiden, setzt Sharp auf eine ähnliche Methode, wobei lediglich die Tiefe der Suche für diese Züge reduziert wird. Sollte sich dann während der Suche herausstellen, dass einer der Züge tatsächlich den Wert des Elternknotens beeinflusst, wird die Suche erneut mit der vollen Tiefe durchgeführt. [7:17] Die Tiefe wird wie folgt reduziert: [7:18]
- Im Wurzelknoten keine Reduktion der ersten 10% an Zügen, danach Reduktion um einen Schritt, für die hinteren 80% Reduktion um zwei Schritte
- Innerhalb des Suchbaumes werden für die Schritte aus Rubrik 5 und 6 (siehe oberer Abschnitt) die Suchtiefe um einen Schritt verringert
Insbesondere gilt somit für Züge, die ausschließlich durch einzelne Schritte in Rubrik 6 generiert werden, dass diese die Suchtiefe insgesamt um vier Schritte verringern (einer pro Rekursionsebene).
Der Entwickler benennt diese Suchtiefenreduktion als einer der Hauptgründe für den Durchbruch von Sharp bei der Arimaa Challenge. Einen großen Teil hierfür leiste die verbesserte Zugsortierung, unter anderem die Generierung der taktischen Züge, um die Suchtiefenreduktion möglich zu machen. [7:19]
¶ Evaluierungsfunktion
Da die Alpha-Beta Suche bei Arimaa in der Praxis nur tiefenbeschränkt ausgeführt werden, benötigen Programme eine möglichst starke Evaluierungsfunktion, welche die Stellungen am Ende der Suche bewertet. Sharp setzt auf eine per Hand erstellte, lineare Evaluierungsfunktion. [7:20] Frühere Versuche eine solche Funktion mit Methoden des maschinellen Lernens zu generieren, waren nur begrenzt erfolgreich. [3:14]
Anders als bei Schach machen feste Bewertungen von Spielfiguren für das Bewerten der Materialien wenig Sinn, da die Funktion von Spielfiguren lediglich von dem relativen Unterschied zu den gegnerischen Spielfiguren abhängig ist. [7:21] Wenn der gegnerische Spieler z.B. keine Figur mehr hat, die stärker als ein Hund ist, gibt es keinen Unterschied in der Funktion und damit Stärke zwischen einem Elefanten und einem Pferd. Um das zu berücksichtigen, verwendet Sharp die "HarLog" Funktion um das Material zu bewerten: [7:22]
wobei und Konstanten sind, die Anzahl an goldenen Hasen, die Anzahl an goldenen Figuren (entsprechend für Silber), die Anzahl Figuren stärker als und genau dann ist, wenn . Die Funktion sei zwar etwas willkürlich, aber korreliere gut mit den Bewertungen von menschlichen Experten. [7:23]
Darüber hinaus berücksichtigt die gesamte Evaluierungsfunktion zahlreiche weitere Parameter, wie den Status der Fallen, die Mobilität der Figuren etc. Als besonders starke Verbesserungen vor dem Sieg bei der Arimaa-challenge, nennt Wu eine Heuristik, welche berücksichtigt, dass Figuren möglichst nahe an den Figuren sein sollten, die sie am effizientesten schlagen (z.B. sollten Pferde nahe an Hunden sein) sowie eine Heuristik um Disbalancen der Spielfiguren auf Regionen des Spielbrettes zu erkennen. [7:24]
¶ Fazit und Ausblick
Der Erfolg von Sharp bei der Arimaa-Challenge hat demonstriert, dass klassische Suchverfahren, wie die Alpha-Beta Suche mithilfe einiger Verbesserungen auch bei Spielen mit enormen Verzweigungsgrad gute Resultate erzielen und menschliche Spieler schlagen können. Insbesondere wird hier die Relevanz von Techniken zur Zerkleinerung des Suchbaumes über das -/-pruning hinaus deutlich. Starke Zugsortierungen kombiniert mit einer Suchtiefenreduktion scheinen dabei besonders effizient zu sein.
2020 schrieb Omar Syed erneut einen Preis von 10.000$ aus, für das erste Programm, welches AlphaZeros Ergebnisse für Arimaa reproduziert und Sharp über 10 Runden besiegt. [10]
¶ Literaturliste
https://en.wikipedia.org/wiki/Arimaa | Zuletzt aufgerufen am: 22.1.2025 19:33 Uhr. ↩︎
https://arimaa.com/arimaa/challenge/ | Zuletzt aufgerufen am: 22.1.2025 19:33 Uhr. ↩︎
Wu, David Jian. Move Ranking and Evaluation in the game of Arimaa. Diss. Harvard University, 2011. | pdf ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
https://en.wikipedia.org/wiki/Computer_Arimaa | Zuletzt aufgerufen am: 22.1.2025 19:36 Uhr. ↩︎
Tomas Kozelek. Methods of MCTS and the game Arimaa. Master’s thesis, Charles University of Prague, Czech Republic, December 2009. | pdf ↩︎ ↩︎ ↩︎
Christ-Jan Cox. Analysis and Implementation of the Game Arimaa. Master’s thesis, Maastricht University, The Netherlands, May 2006. | pdf ↩︎
David J Wu. “Designing a winning Arimaa program”. In: ICGA
Journal 38.1 (2015), pp. 19–40 | pdf ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎Marsland, T. A. (1986). A Review of Game-Tree Pruning. ICGA Journal, Vol. 9, No. 1, pp. 3–19. | pdf ↩︎ ↩︎
David R. Hunter. MM Algorithms for Generalized Bradley-Terry Models. The Annals of
Statistics, 32(1):384–406, 2004. | pdf ↩︎http://arimaa.com/arimaa/forum/cgi/YaBB.cgi?board=devTalk;action=display;num=1596385680 | Zuletzt aufgerufen am: 22.1.2025 16:25 Uhr. Da der Link z.T. nicht lädt alternativ: https://web.archive.org/web/20240807193602/http://arimaa.com/arimaa/forum/cgi/YaBB.cgi?board=events;action=display;num=1577231395 ↩︎