¶ Beschreibung
Der Minimax-Algorithmus ist ein grundlegendes Konzept der Spieltheorie und gehört zur Kategorie der Backtracking-Algorithmen [1]. Er wird verwendet, um optimale Züge für Spieler in Nullsummenspielen mit perfekter Information zu berechnen, wie etwa in Vier Gewinnt, Arimaa oder anderen Zwei-Personen-Spielen. Dabei wird davon ausgegangen, dass beide Akteure stets den optimalen Zug wählen. Die beiden Spieler, bekannt als Maximierer und Minimierer, verfolgen entgegengesetzte Ziele: Der Maximierer versucht die höchstmögliche Punktzahl zu erreichen, während der Minimierer die kleinstmögliche Punktzahl anstrebt.
Die Berechnungen des Minimax-Algorithmus basieren auf einem Spielbaum, bei dem die Knoten Spielzustände sind und die Kanten mögliche Spielzüge darstellen. Jeder Knoten hat entsprechend der Anzahl möglicher Züge eine feste Anzahl von Kindknoten. Es wird zwischen MAX- und MIN-Knoten unterschieden, die jeweils angeben, welcher Spieler am Zug ist. Da die Spieler abwechselnd agieren, alternieren MAX- und MIN-Knoten entlang der Pfade des Spielbaumes.
Der Algorithmus propagiert Bewertungen rekursiv durch den Spielbaum. Für jeden Knoten wird zuerst der Minimax-Wert aller Kindknoten berechnet:
- Ein MAX-Knoten erhält den höchsten Wert seiner Kindknoten
- Ein MIN-Knoten erhält den niedrigsten Wert seiner Kindknoten
Minimax (Knoten, Spieler):
wenn Knoten ein Blatt ist:
gib den Wert des Knoten zurück
wenn Spieler == 1:
maxWert = -∞
für jeden Nachfolger des Knotens:
Wert = Minimax(Nachfolger, -1)
maxWert = max(maxWert, Wert)
gib maxWert zurück
sonst:
minWert = ∞
für jeden Nachfolger des Knotens:
Wert = Minimax(Nachfolger, 1)
minWert = min(minWert, Wert)
gib minWert zurück
¶ Erläuterung
¶ Eingabe
Der Algorithmus erhält zwei Parameter:
- Knoten: Repräsentiert den aktuellen Spielzustand (z. B. ein Spielfeld)
- Spieler: Gibt an, welcher Spieler am Zug ist (1 für den Maximierer und -1 für den Minimierer)
¶ Abbruchbedingung
Ein Knoten gilt als Blatt, wenn der Algorithmus entweder eine festgelegte maximale Suchtiefe erreicht hat oder keine weiteren Nachfolger (Spielzüge) mehr möglich sind.
In diesem Fall wird der Wert des Knotens direkt zurückgegeben. Dieser Wert stammt aus einer heuristischen Funktion, die die Qualität des Spielzustands (z. B. ein Spielfeld) bewertet.
¶ Minimerer
- Initialisierung: Der minimale Wert wird auf ∞ gesetzt
- Iteration: Für jeden möglichen Zug (Nachfolger des Knotens) ruft der Algorithmus rekursiv Minimax auf, wobei der Spieler wechselt (1)
- Minimierung: Der minWert wird aktualisiert, indem der niedrigere Wert zwischen dem aktuellen minWert und dem Wert des Nachfolgers gewählt wird
- Rückgabe: Der niedrigste Wert unter allen möglichen Nachfolgern wird zurückgegeben
¶ Maximierer
- Initialisierung: Der maximale Wert wird auf -∞ gesetzt
- Iteration: Für jeden möglichen Zug (Nachfolger des Knotens) ruft der Algorithmus rekursiv Minimax auf, wobei der Spieler wechselt (-1)
- Maximierung: Der maxWert wird aktualisiert, indem der höhere Wert zwischen dem aktuellen maxWert und dem Wert des Nachfolgers gewählt wird
- Rückgabe: Der höchste Wert unter allen möglichen Nachfolgern wird zurückgegeben
¶ Ergebnis
Die Lösung des Spielbaumes ist der Minimax-Wert der Wurzel. Dieser gibt an, welcher Wert erzielt wird, wenn beide Spieler stets die bestmöglichen Züge wählen. Der daraus resultierende Pfad zwischen Blattknoten und Wurzel, welcher diesen Wert enthält, wird als Principal-Variation bezeichnet. [2].
¶ Bewertung eines Spielzustands
Die Bewertung eines Knotens erfolgt durch eine heuristische Funktion, die eine Spielsituation auf einen numerischen Wert abbildet. Positive Werte deuten auf einen Vorteil des Maximierers hin, negative Werte auf einen Vorteil des Minimierers. Beträge nahe null weisen auf eine ausgeglichene Spielsituation hin. Die Blattknoten werden direkt durch die Heuristik bewertet. Innere Knoten erhalten ihre Bewertung hingegen durch die Propagation der Werte ihrer Kindknoten.
Die endgültige Entscheidung, die vom Minimax-Algorithmus getroffen wird, hängt davon ab, wie gut die heuristische Funktion ist. Daher ist es von größter Bedeutung, eine vernünftige heuristische Funktion zu entwerfen[3]. Beispiele für Bewertungen von Spielzuständen sind im Artikel von Vier Gewinnt zu finden.
¶ Beispiel
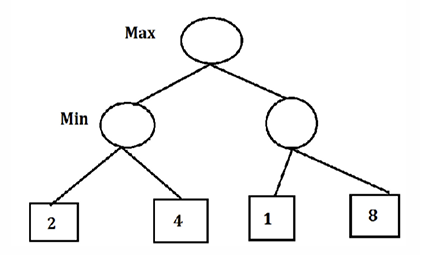
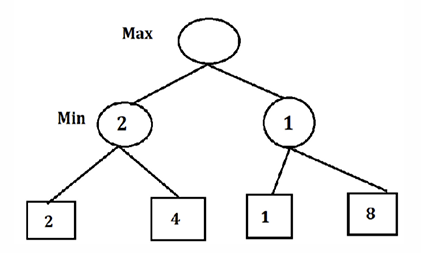
Betrachten wir folgendes Beispiel von Nasa et al.[4] in Abbildung 1 und Abbildung 2 mit einem perfekten Binärbaum, der vier Endzustände aufweist. Diese vier Blätter können vom Wurzelknoten aus über verschiedene Pfade erreicht werden. Der erste Spieler, der einen Zug macht, befindet sich an der Wurzel. Angenommen, der maximierende (oder minimierende) Spieler macht den ersten Zug, dann befindet sich dieser an der Wurzel, während der Gegner auf der nächsten Ebene spielt. Ein interessantes Merkmal dieses Szenarios ist, dass der Zug des maximierenden (oder minimierenden) Spielers davon abhängt, dass der Gegner ebenfalls optimal spielt.
Die Entscheidung des Spielers wird getroffen, nachdem alle möglichen Züge überprüft wurden. Zu Beginn hat der Maximierer die Wahl, entweder nach links oder nach rechts zu ziehen. Angenommen, der Maximierer wählt den linken Pfad, so ist der Minimierer an der Reihe. Der Minimierer hat nun die Wahl zwischen den Werten 2 und 4. Da das Ziel des Minimierers ist, den Wert zu minimieren, wählt er den kleineren Wert, also 2.
Anschließend zieht der Maximierer nach rechts, und der Minimierer muss nun zwischen den Werten 1 und 8 wählen. Der Minimierer wird in diesem Fall 1 wählen, da er den niedrigeren Wert bevorzugt. Nun ist es erneut der Maximierer, der zwischen den Werten 2 und einem anderen Wert wählen muss. Da das Ziel des Maximierers ist, den höchsten Wert zu erreichen, wählt er den größeren der beiden Werte, also 2. Dies ist in Abbildung 2 verdeutlicht.
Am Ende erhält der Maximierer den optimalen Wert von 2, was beduetet, dass der Spieler bei Suchtiefe 2 den größten Vorteil erhält, wenn er nach links geht.
¶ Negamax
Der klassische Minimax Algorithmus besteht aus zwei Teilen: einem für den minimierenden Spieler und einem für den maximierenden Spieler. Je nach Knotenart (MIN oder MAX) erhält der Knoten den Wert des Kindknotens mit dem minimalen bzw. maximalen Wert. Diese beiden Teile können zu einer einzigen Komponente zusammengefasst werden, indem das Minimierungsproblem des minimierenden Spielers in ein Maximierungsproblem umgewandelt wird. Dazu wird einfach die Bewertung für den minimierenden Spieler negiert, sodass nun beide Spieler jeweils ein Maximierungsproblem lösen. Diese vereinfachte Version wird als Negamax bezeichnet.
negamax(Knoten):
wenn Knoten ein Blatt ist:
gib den Wert des Knotens zurück
Wert = −∞
für alle Kinder von Knoten:
Wert = max(Wert, −negamax(Kind))
gib Wert zurück
¶ Laufzeit
Wie man im Beispiel erkennt, muss der Algorithmus jeden Knoten im Baum besuchen. Die Zeitkomplexität eines Minimax-Suchalgorithmus ist daher , wobei b der Verzweigungsfaktor oder die Anzahl der legalen Züge an jedem Punkt und m die maximale Tiefe des Baums ist[5].
Die Laufzeit des Minimax-Algorithmus ist exponentiell zur Suchtiefe, was zu einer schnellen Zunahme der Berechnungsdauer führt und in vielen Fällen zu einer unpraktikablen Laufzeit. Beim Beispiel von Vier Gewinnt gibt es etwa 4,5 Billionen gültige Spielzustände [2:1]. Diese Anzahl an Zuständen macht es praktisch unmöglich, alle möglichen Züge zu berechnen, weshalb Optimierungen des Algorithmus erforderlich sind, um die Effizienz zu steigern.
Ein gängiges Verfahren zur Laufzeitverbesserung ist das Alpha-Beta Pruning, bei dem unnötige Zweige des Suchbaums, die keine Auswirkung auf das Endergebnis haben, abgeschnitten werden. Dadurch wird die Anzahl der zu untersuchenden Zustände reduziert[6].
¶ Referenzen
Anmerkung: Diese Seite wurde von Marin Dvojkovic verfasst. Änderungen von anderen Personen an diesem Artikel sind nicht mit dem Verfasser abgesprochen.
¶ Abbildungen
Pseudocode 1 übersetzt aus: Carl Felstiner. 2019. Alpha-beta pruning. [6:1]
Pseudocode 2 übersetzt aus: Yassin Liese. 2024. Entwicklung eines Frameworks zur systematischen Evaluierung und Optimierung Minimax-basierter Suchstrategien anhand des Spiels Vier-Gewinnt. [2:2]
Abbildung 1 aus: Rijul Nasa, Rishabh Didwania, Shubhranil Maji, and Vipul Kumar. 2018. Alpha-beta pruning in mini-max algorithm–an optimized approach for a connect-4 game.[4:1]
Abbildung 2 aus: Rijul Nasa, Rishabh Didwania, Shubhranil Maji, and Vipul Kumar. 2018. Alpha-beta pruning in mini-max algorithm–an optimized approach for a connect-4 game.[4:2]
¶ Textquellen
James R. Bitner and Edward M. Reingold. 1975. Backtrack programming techniques. Commun. ACM 18, 11 (November 1975), 651–656. https://doi.org/10.1145/361219.361224 ↩︎
Yassin Liese. 2024. Entwicklung eines Frameworks zur systematischen Evaluierung und Optimierung Minimax-basierter Suchstrategien anhand des Spiels Vier-Gewinnt. Technische Universität Berlin, Berlin. Retrieved January 16, 2025 from https://doc.neuro.tu-berlin.de/bachelor/2024-BA-YassinLiese.pdf ↩︎ ↩︎ ↩︎
Xiyu Kang, Yiqi Wang, and Yanrui Hu. 2019. Research on different heuristics for minimax algorithm insight from connect-4 game. Journal of Intelligent Learning Systems and Applications 11, 02 (2019), 15. ↩︎
Rijul Nasa, Rishabh Didwania, Shubhranil Maji, and Vipul Kumar. 2018. Alpha-beta pruning in mini-max algorithm–an optimized approach for a connect-4 game. Int. Res. J. Eng. Technol 5, (2018), 1637–1641. ↩︎ ↩︎ ↩︎
Abdoul Wahab Touré. 2023. Evaluation of the Use of Minimax Search in Connect-4 —How Does the Minimax Search Algorithm Perform in Connect-4 with Increasing Grid Sizes? AM 14, 06 (2023), 419–427. https://doi.org/10.4236/am.2023.146025 ↩︎
Carl Felstiner. 2019. Alpha-beta pruning. Whitman College (2019). Retrieved January 16, 2025 from https://www.whitman.edu/documents/Academics/Mathematics/2019/Felstiner-Guichard.pdf ↩︎ ↩︎